I made my code take a parameter for the number of triangles (n) and show it's value in the figure caption.

This is what it looks like with n = 128.

The LaTeX code is here: https://www.overleaf.com/read/scsptwzqxzdt.

#math #maths #spiraloftheodorus

"The most amazing property of the square root spiral is surely the fact that the distance between two successive winds of the Square Root Spiral quickly strives for the well known geometrical constant π !!
···
Another striking property of the Square Root Spiral is the fact, that the square roots of all square numbers (4, 9, 16, 25, 36…) lie on 3 highly symmetrical spiral graphs which divide the square root spiral into three equal areas..."

Interesting.

#math #maths #spiraloftheodorus #squarerootspiral

References
--------------
[1] "The Ordered Distribution of Natural Numbers on the Square Root Spiral", https://arxiv.org/abs/0712.2184

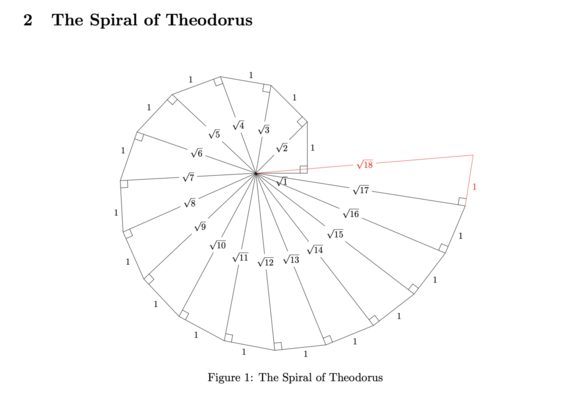
I've updated this figure again to show the fact that the triangles of the spiral begin to overlap when the hypotenuse equals √18. Basically I moved where the √1 (first triangle) is so it is consistent with the other hypotenuses.

The pdf is here: https://davidmeyer.github.io/qc/spiral_of_theodorus.pdf. The LaTeX source is here: https://www.overleaf.com/read/scsptwzqxzdt. As always, questions/comments/corrections/* greatly appreciated.

#math #maths #spiraloftheodorus

References
--------------
[1] "Spiral of Theodorus", http://jwilson.coe.uga.edu/EMAT6680Fa2012/Nelli/spiraloftheodorus/spiraloftheodorus.html

[2] "Here's some math/LaTeX/TikZ fun for today: The Spiral of Theodorus", https://www.facebook.com/dmm613/posts/pfbid02PiH3FeCNPaLK6G9hTuqCqcMG8JGSFxKx6Mze7pXDfDtdvPqZCHx2cm1V8dpnaUUml

Did you know that the √17 hypotenuse of the the Spiral of Theodorus belongs to the last triangle that does not overlap in the spiral?

What is so special about the number 17?

Interestingly, Theodorus used this spiral to prove that all non-square integers from 3-17 are irrational and the original spiral stops at √17, apparently because that is the last hypotenuse before overlapping the rest of the figure [1].

In 1958 E. Teuffel proved that no two hypotenuses of the spiral of Theodorus will ever coincide, regardless of how far the spiral is continued. Apparently this was proved in "Eine Eigenschaft der Quadratwurzelschnecke", Math.-Phys. Semesterber. 6 (1958), pp. 148-152. I can't identify the journal, though my hunch is it's Mathematische Semesterberichte (does anyone have access to a copy of this paper?).

Pretty incredible.

I've updated my figure (see below) to acknowledge the fact that the triangles of the spiral start to overlap at √18.

The updated pdf is here: https://davidmeyer.github.io/qc/spiral_of_theodorus.pdf.
The updated LaTeX code is here: https://www.overleaf.com/read/scsptwzqxzdt.

As always, questions/comments/corrections/* greatly appreciated.

#math #maths #spiraloftheodorus #Irrationalnumbers

References
--------------
[1] "Spiral of Theodorus", http://jwilson.coe.uga.edu/EMAT6680Fa2012/Nelli/spiraloftheodorus/spiraloftheodorus.html

Here's some math/LaTeX fun for today: The Spiral of Theodorus

What is the Spiral of Theodorus?

The Spiral of Theodorus [1] is the fantastic object shown below. It is composed of right triangles placed edge-to-edge, where the side opposite the (inside) acute angle has length 1 and where the length of the hypotenuse of the n^{th} triangle is √(n+1). Pretty cool.

The spiral is named after Theodorus of Cyrene, the ancient Greek mathematician who lived during the 5th century BC and who apparently discovered the spiral [2].

So can you draw the Spiral of Theodorus in tikz? But of course! I don't know if I love the approach I used to draw the figure below (I've tried a few different approaches), but this is where I stopped...

A few of my notes are here: https://davidmeyer.github.io/qc/spiral_of_theodorus.pdf. The LaTeX source is here: https://www.overleaf.com/read/scsptwzqxzdt.

#TeXLaTeX #spiraloftheodorus #math #maths

References
--------------
[1] "Spiral of Theodorus", https://en.wikipedia.org/wiki/Spiral_of_Theodorus