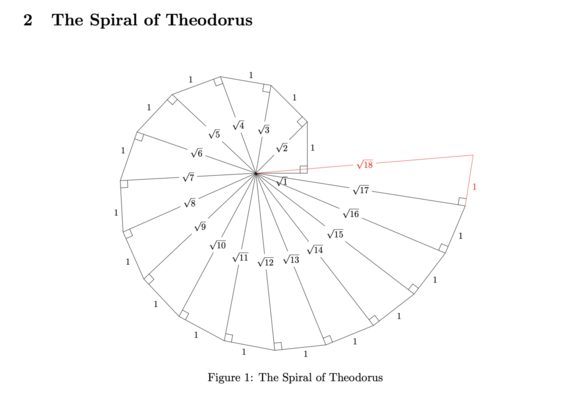
Did you know that the √17 hypotenuse of the the Spiral of Theodorus belongs to the last triangle that does not overlap in the spiral?

What is so special about the number 17?

Interestingly, Theodorus used this spiral to prove that all non-square integers from 3-17 are irrational and the original spiral stops at √17, apparently because that is the last hypotenuse before overlapping the rest of the figure [1].

In 1958 E. Teuffel proved that no two hypotenuses of the spiral of Theodorus will ever coincide, regardless of how far the spiral is continued. Apparently this was proved in "Eine Eigenschaft der Quadratwurzelschnecke", Math.-Phys. Semesterber. 6 (1958), pp. 148-152. I can't identify the journal, though my hunch is it's Mathematische Semesterberichte (does anyone have access to a copy of this paper?).

Pretty incredible.

I've updated my figure (see below) to acknowledge the fact that the triangles of the spiral start to overlap at √18.

The updated pdf is here: https://davidmeyer.github.io/qc/spiral_of_theodorus.pdf.
The updated LaTeX code is here: https://www.overleaf.com/read/scsptwzqxzdt.

As always, questions/comments/corrections/* greatly appreciated.

#math #maths #spiraloftheodorus #Irrationalnumbers

References
--------------
[1] "Spiral of Theodorus", http://jwilson.coe.uga.edu/EMAT6680Fa2012/Nelli/spiraloftheodorus/spiraloftheodorus.html

In 1768, Johann Heinrich Lambert and Ferdinand von Lindemann proved that it is impossible to ”square the circle.” #Poetry #Science #History #Mathematics #Pi #IrrationalNumbers #Lambert #vonLindemann (https://sharpgiving.com/thebookofscience/items/p1768.html)

#PiDay #IrrationalNumbers
https://youtu.be/RqlSG9CyaQU

@johncarlosbaez

XD

But....now I wonder if there is such a thing as "finding an infinite non-repeating sequence in reverse" and if that applies to digits of irrational numbers!

Surely not right? XD
But...I mean it would still have an infinite number of digits, and never repeat..

And we think of "a circle of infinite radius" as a line, and other things as "at infinity looking back"...

dlfkjfldkfjdlfk *is* it possible?

#maths #infiniteSequences #irrationalNumbers

Why π^π^π^π could be an #integer (for all we know!)

https://www.youtube.com/watch?v=BdHFLfv-ThQ&ab_channel=Stand-upMaths

#Pi #Maths #Math #Mathematics #Algebra #Fractions #IrrationalNumbers #TranscendentalNumbers #Computing #LargeNumbers #Computation #ComputingPower

A lovely post on Dirichlet’s approximation theorem, which allows you to approximate irrational number with rational numbers with small denominators with guarantees on how close the irrational number is the approximation.

https://www.quantamagazine.org/how-rational-math-catches-slippery-irrational-numbers-20200310/

#Mathematics #Numbers #RationalNumbers #IrrationalNumbers #NumericalApproximations