6/

In general, the smoothly-connecting double cusp groups with numerator k are clustered into groups where the denominator is of the form \(kn + m, m < k \); m, k co-prime.

So, for example:

- if k=4, m ϵ {1,3}
- if k=5, m ϵ {1,2,3,4}
- if k=6, m ϵ {1,5}
- if k=7, m ϵ {1,2,3,4,5,6}
- if k=8, m ϵ {1,3,5,7}

There are always an even number of such sub-streams, and they come in complementary pairs (where m=j, k-j) where the structure is similar, but complementary. For example, when k=7, the paired streams are {7n+1, 7n+6}, {7n+2, 7n+5}, {7n+3, 7n+4}.

Attached are several movies that show this effect when the numerator is 7.

- the first one, titled "7n-Smoosh", shows what a concatenation looks like that includes all denominators in order, with maximum denominator 150

- the other three are titled "7n+1", "7n+2", and "7n+3" with maximum denominator 250

As was the case for the case where the numerator is 3, the relative beauty of these videos is in the eye of the beholder, but the ones that are constrined to constant offsets of a multiple of the numbeator are much more consistent to one another.

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #mathart #mastoart #perfectloops

5/

Attached are three different traces of the Maskit projection through the double-cusp groups where the numerator is 3, with a cap on the denominator at 188.

The first attached video (whose caption begins with "Smoosh") shows the result of concatenating every available cusp, sorted by increasing value of the corresponding fraction; that is, the cusp list starts with {3/188, 3/187, 3/185, 3/184 ...}. Note that there is no double-cusp group for 3/189 or 3/186 because those fractions reduce.

Unlike the movies for numerators 1 and 2, in this case the animation looks quite choppy and, although visual appeal is a matter of taste, certainly does not minimize differences between frames.

The second and third videos show the technique to generate smooth animations. Since that the frames corresponding to cusps expressed as 3/(3n + 1) share an orientation, as do the cusps 3/(3n + 2), we must render two separate movies, one for each pattern, to get a smooth animation.

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #mathart #mastoart #perfectloops

4/

Attached are gifs of the Maskit, Jorgensen, and Unit Circle projections of the 2/(2n+1) cusps where 1 <= n <= 63 (yielding cusps ranging from 2/3 to 2/127.

There are't any cusps with even denominators because the numerator and denominator associated with a double cusp group must be coprime.

A few things are retained from the animations through the 1/n groups from previous posts : each projection seems to converge to a final visible shape quite quickly, and as the palette size shifts relative to the value of n, the color patterning shifts in a consistent way between all three projections.

Interestingly, in both the 1/n case and the 2/(2n+1) case, the color gradients are most distributed for half-multiples of the palette size and most concentrated at multiples of the palette size (60 in these renders). So 2/61 has similar colors to 1/30 (palette size=60), and 2/167 has similar colors to 1/63, across all projections.

Next time we'll do the same thing for the double cusp groups where the numerator is 3. You're invited to speculate about whether there will be any surprises...

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #mathart #mastoart #perfectloops

3/

The previous post showed an effect where color gradients for 1/n cusps are highly concentrated when n is a multiple of the palette size, and widely distributed when n is a half-multiple of the palette size. This effect appeared to be conserved across projections.

Attached are 4 images demonstrating that this effect appears to also be conserved under resizing the desired output image. I found this far more counter intuitive than conservation across projections -- after all, the value of ε is half as much as it was for the smaller renders, you'd expect that to affect the depth needed to get to a terminal node. Honestly, I don't have a great explanation for it; any actual topologists who want to weigh in with your two cents, please consider yourselves invited.

The attached still images are 1920x1080 and 960x540 renders of the Unit Circle projections of the 1/31 and 1/63 cusps; the larger ones have more detail, but still show the same color gradient distribution pattern.

The 1920x1080 animations are too large to host on Mastodon; the YouTube links follow; the only parameter changing between these and the animations posted earlier in this thread is the image size.

Jorgensen: https://youtu.be/lEY6yWwDT74

Unit Circle: https://youtu.be/Y1rczGsU9Hk

Maskit: https://youtu.be/CMb7OdDTH1o

Some of you (my favorites) are skeptically thinking "she's asserting that this happens on multiples and half-multiples of palette size, but she's only showing one of each."

Unit Circle Looping up to 1/189 cusp: https://youtu.be/mNRp74Pe8b4

Traversal in R, rendering using Cairo, movie conversion with ffmpeg.

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #mathart #mastoart #perfectloops

2/

Attached see the same animations as in the first post in this thread, with the important exception that they are in different projections (the unit circle reference projection and the Maskit projection).

Just like the Jorgensen projection presented last time, these show the double cusp groups 1/n, where n is { 2, 3, 4, ... 63, 62, 61 ... 4, 3, 2 }. The palette (length 60) and color assignment rules similarly are the same.

At first it seems like quite a coincidence that the colors behave the same way with respect to n (that is, showing the most variation when n is a half-multiple of the palette size, the least when n is a multiple of the palette size), but it made sense (at least to me) after some reflection.

The underlying structure and topology of these projections are the same, so the node depth needed to draw what our minds perceive as the preserved elements from frame to frame proceeds the same way.

Interestingly, this phenomenon is conserved across resolutions as well, so renders of these groups at, say, 1920x1080, show the same high-level color patterning behavior (I'll post a demo later on YouTube).

Traversal in R, rendering using Cairo, movie conversion with ffmpeg.

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #mathart #mastoart #perfectloops

2/

Attached see two more versions of the same animation as in the first post in this thread. These ones use the unit circle reference projection and the Maskit projections, though.

Just like the Jorgensen projection presented last time, these show the double cusp groups 1/n, where n is { 2, 3, 4, ... 63, 62, 61 ... 4, 3, 2 }. The palette (length 60) and color assignment rules similarly are the same.

At first it seems like quite a coincidence that the colors behave the same way with respect to n (that is, showing the most variation when n is a half-multiple of the palette size, the least when n is a multiple of the palette size), but it made sense (at least to me) after some reflection.

The underlying structure and topology of these projections are the same, so the node depth needed to draw what our minds perceive as the preserved elements from frame to frame proceeds the same way.

Interestingly, this phenomenon is conserved across resolutions as well, so renders of these groups at, say, 1920x1080, show the same high-level color patterning behavior (I'll post a demo later on YouTube).

Traversal in R, rendering using Cairo, movie conversion with ffmpeg.

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #mathart #mastoart #perfectloops

1/

The next few posts are going to explore how to arrange limit sets in time to make movies that appeal to human eyes. So far the animations on this channel have varied granularity ε or the μ parameter that defines the topology of the limit set.

This movie, and the ones following in this thread, consists simply of concatenations of double cusp limit sets, so there is no continuous movement to model.

However, to our visual systems there is a "preferred" way to sequence double-cusp groups that is appealing, and conserved across projections.

The art tax for this post is a simple example of a pleasing path: a looped animation of the Jorgensen tb=2 projection for the cusps 1/n, where n is { 2, 3, 4, ... 63, 62, 61 ... 4, 3, 2 }.

The palette and the rules for choosing line colors (by the depth of the terminal node in the tree associated with those line segments) do not change at all from frame to frame. In this case the palette size was 60.

The apparent color-cycling behavior comes about because the shapes that our minds map as "the same" from one frame to the next have a consistently increasing tree depth associated with them.

To look at this a little more closely, see the attached still image, which shows how the structure of the limit set changes as n varies. Each step along the path is the transformation of the previous circle by a group generator. For the 1/n cusp, for walking this path, we apply the loxodromic/spiral generator a (or A) n times, before applying the parabolic generator B (or b).

Traversal in R, rendering using Cairo, movie conversion with ffmpeg.

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #mathart #mastoart #perfectloops

This is the fifth and final post in a series arising from the Fibonacci cusps of Kleinian double-cusp groups.

The art for this post is an ε-descent movie of the Golden Mean Group's Jorgensen projection. Unlike the other ε-descent movies, this one goes deep into the subpixel range, from 2px down to 0.01px (that is, 200x finer required granularity than the other ones). And it's clear that it's far from done revealing visible features.

Notice how you can still follow the downward paths as they trace out the Fibonacci sequence with their hairpin turns: 1-1-2-3-5 etc, but this time there isn't a final value where they will flatten out and join one another

The entire 150-frame movie took about 10 days to render; the initial frames took about 8 seconds apiece when ε~2. The final three frames, at ε~{1.012, 1.011, 101} took {24h, 28h30m, 36h) to render : over 40% of the total rendering time!

This is an example of malicious compliance by a mathematical object: it is associated with a point on the Maskit Curve, so its features do have to shrink as you descend the tree. And in the limit it will converge on being constructed entirely out of completed tangent circles, and those emergent circles will close, but it's going to take literally as long as possible to get there.

There are infinitely many other such irrational groups along the Maskit Curve which I, following the example of Pythagoras, will proceed to disregard in favor of the far-more-tractable rationals.

End of thread.

Traversal in R, rendering using Cairo, movie conversion with ffmpeg.

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #mathart #fibonacci #mastoart

#fibonaccicusps

This is the fourth in a series of posts arising from the Fibonacci cusps of Kleinian double-cusp groups.

The last post asked "why does the Golden Mean group clearly have more visible features to reveal when rendered at ε=1/40px, while the Fibonacci cusps that converge to it are done showing new visible features when ε gets down to about 2 pixels?" (see https://mathstodon.xyz/@KleinianArborist/110685414981687380)

The attached video shows an ANALOGY for the difference between "rational" vs "irrational" numbers on the Maskit curve (longer version: https://youtu.be/9FvB8WWlYPY).

It shows side-by-side renders of the first few Fibonacci cusps (Unit Circle projection) as their required granularity decreases (the bar in the middle visually displays the value of ε).

On the right the "emergent circles" close immediately, whereas on the left they never quite meet. Circles happen when an infinite word in the group has the property of "parabolicity".

All the parabolic words for double-cusp groups are predictable and repeating (by analogy, rational numbers always repeat their digits). The groups corresponding to irrational numbers also have an infinite number of parabolic words, but they're not predictable.

The image on the right has these "special words" included in the ordered list of points for each node, the left does not. Those special words make the emergent circles.

Traversal in R, rendering using Cairo, image editing in gimp.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms
#mathematicalart #generative #generativeart #mathart #fibonacci
#fibonaccicusps

This is the third in a series of posts arising from the Fibonacci cusps of Kleinian double-cusp groups.

As previously discussed, a series of fractions Fib(n)/Fib(n+1) will tend towards 1/ϕ over time. Correspondingly, the sequence of Fibonacci cusps on the Maskit curve will converge to the point corresponding to 1/ϕ, which generates what I suppose might be called the Golden Mean Group.

The μ parameter for this group for the Maskit slice where the second and fourth generators are parabolic ("tb=2") is provided in [1], specifically μ=1.2943265032+1.6168866453i (there is a mirror group with essentially the same properties at μ=0.7056734968+1.6168866453i). Curt McMullen and Troels Jorgensen were major proximate contributors to nailing this down.

Attached are Maskit and Jorgensen renders of the Golden Mean group. Interestingly, this set doesn't meet up like the Fib cusps that led up to it, even though the value of ε was set extremely low It looks like one of the intermediate frames from the walk animations, not a proper group. But what there still seems to be made up of tangent circles. What's going on? We'll start to explore that in the next post.

A completely different take on rendering this group is found in [1], fig 10.4 which is definitely worth a look if you're interested..

Traversal in R, rendering using Cairo, image editing in gimp.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #generative #generativeart #mathart #fibonacci #fibonaccicusps

This is the second in a series of posts arising from the Fibonacci cusps of Kleinian double-cusp groups.

One of the more endearing properties of the double-cusp groups is that they don't hold anything back; once you know how, you can read which group they are right off the image.

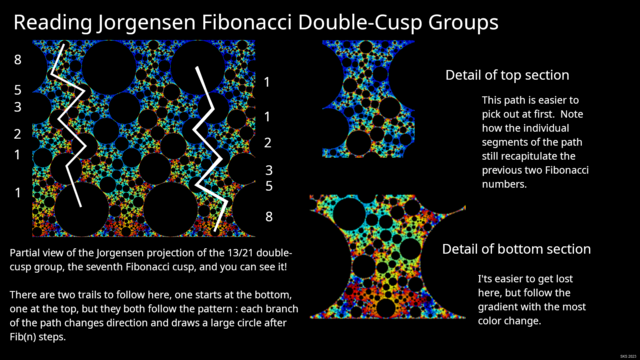
Remember how last post we were imagining jumping further and further down to the next Fibonacci cusp (1/1, 1/2, 2/3,3/5...), switching directions each time? Well, let's take a look and see what the groups themselves are telling us.

The attached image contains a selection from the Jorgensen projection of the 13/21 cusp, with a couple of paths marked through the set. If you compare to the animations in the previous post, you'll recognize the downward-tracing path as the one that's "always there". while the upward-tracing path is the one that "emerges" as you land exactly on the double-cusp point.

Note that the fractal repeats itself horizontally, so you can use the extra copy of each path in the image to follow the trace; for the later parts of the path, refer to the detail images on the right.

Pretty slick that our mental model of jumping left and right from cusp to cusp along higher and higher fibonacci counts has resulted in an image that does the same thing! Almost as though that metaphor was chosen for just that reason...

Traversal in R, rendering using Cairo, image editing in gimp.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #generative #generativeart #mathart #fibonacci #fibonaccicusps

This is the first in a serious of posts arising from the Fibonacci cusps of Kleinian double-cusp groups.

The attached static image is an illustration of the Maskit slice; if you draw a line along the topmost points in this plot, it cuts the plane into two regions: above it groups are discrete (and, among other things, are amenable to the ε-termination tool from last time), below it most groups are chaotic (plotted points being the exceptions).

Each point on the Maskit curve itself corresponds to a point on the real line between 0 and 1, inclusive; by convention we refer to those points that correspond to rational numbers "cusps"; they not only literally stand out from the curve, but also generate very appealing images made up entirely of tangent circles. But there are ofc infinitely more points that correspond to irrational numbers.

If you imagine perching on the top-right hand side spot at 2+2i, then jumping down and to the left to the next prominent cusp, then down and to the right, then left again, you'll visit:

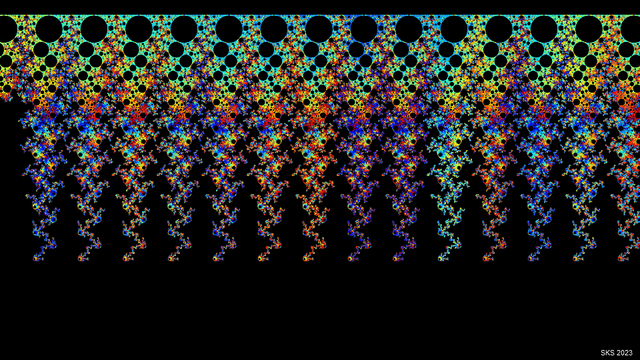
1/1, 1/2, 2/3, 3/5, 5/8. 8/13 ...

These are the Fibonacci cusps, if you follow the path forever, it implies that you'll eventually converge on the point associated with 1/ϕ.

Art tax: Jorgensen and Maskit projections going through the first seven Fibonacci cusps and back.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

[2] image credit : Curtis McMullin's web page at https://people.math.harvard.edu/~ctm/gallery/teich/maskit.gif

[3] https://en.wikipedia.org/wiki/Bers_slice

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #generative #generativeart #mathart #fibonacci #fibonaccicusps

When using a DFS to draw a Kleinian limit set, you partially traverse an infinite 3-ary tree. Each node corresponds both to a particular word in a 4-letter alphabet and an ordered set of points. Line segments can be drawn connecting those points in order; the deeper you go into the tree before drawing, the more detail you get. But when do you stop?

Many visually-appealing groups have the property that the node path length monotonically decreases as you descend any particular path, making "ε-termination" quite useful : when the distance along the a node's path is less than a provided value ε, draw and terminate.

The optimal ε depends on the size of your pixels in math space, your drawing technique (for example, in general a higher-ε wants a higher line width), and how much quality you want.

Attached is an animation showing how the renders of three different Kleinian limit sets change as the {ε, line width} parameters are decreased from {500 pixels, 4.5 pixels} to {2 pixels, 0.5 pixels}. An animation with more limit sets included is available at https://www.youtube.com/watch?v=gH4kacpgw_A.

The groups shown are :

- Riley group with parameter c=0.05+0.93i
- Jorgensen projection of the 3/31 double-cusp group
- Jorgensen group with parameters ta=1.87+0.1i, tb=1.87-0.1i

I wrote the rendering code in R, used Cairo to export to .png, and ffmpeg to convert to .mp4.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #generative #generativeart #mathart

As scaffolding for a larger project, I had to figure out how to uniquely enumerate the generalized circles that make up any double-cusp Kleinian limit set, and determine their representative matrices.

Once I had my hands on that, it seemed natural to use those open interior spaces to recursively nest other limit sets.

The enclosing limit set is a 0/1 cusp displayed in the unit-circle reference projection described in _Indra's Pearls_. The nested limit sets were picked by starting at a random location in a large Farey sequence and simply using sequential elements.

The coloration comes from drawing the line segments based on how long the word associated with their corresponding terminal node is; this render used a palette of length 50, and flips the order of traversal at each nesting layer.

I wrote the rendering code in R, and rendered to .png using Cairo.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart

The design is based on a puffer that occurs in the Life-like cellular automaton B368/S245, which I deconstructed to show all 171 states of the pattern and set to a rainbow colormap. #generativeart #mathematicalart #art #tshirt

local non-euclidean | global euclidean
—
rearrangement of surfaces resulted from cutting a special torus (R=a; r=a/2) and alternating them by curvature type.
—
#abstractart #algorithmicart #codeart #computerart #contemporary_art #creativecoding #digitalart #submillimetre #generativedesign #generativeart #geometry #mathart #mathematicalart #minimalart #modernart #3d #monochrome #opticalart #3dmodel #3drender #shader #topology #abstractdesign #parametricdesign #rhino3d #opart #computationaldesign

I hate #introduction but here’s an attempt:

👋, I am Poulami.

By trade, I am a #UXDesigner interested in #accessibility #privacy, #EthicalDesign.

In hobbies: #MathematicalArt,#CreativeCoding,#CSSart (https://poulamic.com/).

I am curious about everything. Twitter expanded my worldview and helped me reevaluate a lot of my opinions. I hope that continues here.

For most part - in real life and on SM - I have been a wallflower. With this fresh start, I am hoping to be a tad more active🤞.

👋

I am Poulami.

By trade, I am a #UXDesigner interested in #accessibility, #Privacy and #EthicalDesign.

In hobbies: #MathematicalArt/#GeometricArt,#CreativeCoding,#CSSart (https://poulamic.com/).

Twitter expanded my worldview and helped me reevaluate a lot of my opinions - about history, society, politics, ecology and about myself. I hope that continues here.

For most part - in real life and on SM - I have been a wallflower. With this fresh start, I am hoping to be a tad more active🤞.

Noise Bullseye

Experimenting with semi-random noise in Processing. In this generative art piece I programmed it so that each pixel has a random lightness and the lightness is biased towards a certain value. That value is determined by the sine function, which is plotted in polar coordinates.

You'll notice that there are rings of pure black... This is due to the value of the sine function being zero (I used sin( r/20 ) + 1 so the the area where the sine is zero is stretched out) and the fact that the lightness of each pixel is obtained by multiplying by the sine function. So the lightness of these pixels is a random value multiplied by the sine at that location, which ends up being zero.

I like how the result ended up looking like a 3D styrofoam bullseye.

#Art #ArtistOfMastodon #Abstract #AbstractArt #Generative #GenerativeArt #Math #MathArt #Maths #Mathematics #MathematicalArt #Geometry #Geometric #GeometricArt #Coding #Programming #Algorithm #Processing