Colin the Mathmo · @ColinTheMathmo
4636 followers · 21174 posts · Server mathstodon.xyzHere's a great problem from Donald Bell ... can you solve it?
========
Rectangling the Square:
Is there a set of rectangles, with no repeated length of side, that will tile more than one rectangle?
========
To get the context of the problem you'll need to read Donald's DOCX ... I'm not really in a position to extract and reformat it, but I'm hosting a copy here:
http://www.solipsys.co.uk/documents/DonaldBell_RectanglingTheSquare.docx
Love to hear your ideas !!
#MathsPuzzle #GeometryPuzzle #MTBoS
(Boosts welcome for reach)
#mtbos #geometrypuzzle #MathsPuzzle
Colin the Mathmo · @ColinTheMathmo
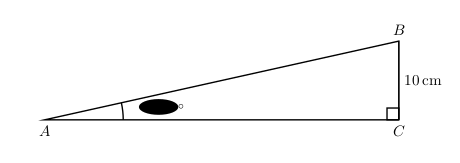
4293 followers · 19469 posts · Server mathstodon.xyzAn interesting and original (I think) puzzle from Micky Bullock.
Last week Negligent Neil calculated length AC. He had forgotten to switch his calculator from radians to degrees but, fortunately, he still got the answer right.
An inky splodge has now obscured the angle at A. Negligent Neil has forgotten what his answer was for length AC, but he insists it was between 40 cm and 50 cm.
Find length AC to 3 significant figures.
#maths #math #puzzle #trigonometry #MathsPuzzle #mathpuzzle
Robert Sundling · @mrwizard
26 followers · 29 posts · Server mathstodon.xyzHere’s another “find the flaw in this proof” puzzle I made for my nieces and nephews, similar to the earlier ones I shared. This one is for younger children, who have just learned squares and square roots. It is relatively simple and requires them to have only one extra bit of mathematical knowledge to solve it. #MathPuzzles #MathsPuzzle
Mr. Wizard · @mrwizard
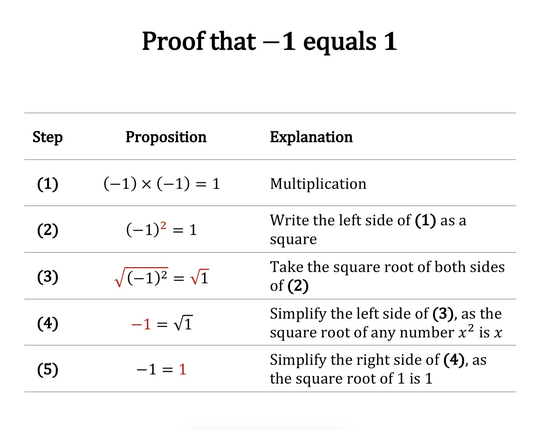
17 followers · 8 posts · Server mathstodon.xyzHere is another “proof with an error” I made for my nieces and nephews, as a puzzle for them to solve. Spot the problem! I used this simplified proof to help demonstrate the basic idea of the flaw in the earlier one – https://mathstodon.xyz/@mrwizard/109526543494924301 – in a way they could understand with just algebra. #MathsPuzzle #MathPuzzles
Mr. Wizard · @mrwizard
7 followers · 3 posts · Server mathstodon.xyzSometimes, I like to present intentionally-flawed proofs to my nieces and nephews to see if they can find the problem. Here’s one that they recently enjoyed. #MathsPuzzle #MathPuzzles
TeacherBowTie · @TeacherBowTie
45 followers · 30 posts · Server mathstodon.xyz@ColinTheMathmo Thanks for the welcome, and the advice.
Here is, I think, the answer to your #MathsPuzzle.
I played with the numbers for a bit before deciding that it was unlikely there would be more solutions, and then tried to justify why.