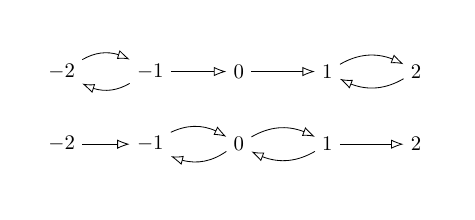
@standefer I suppose, when one is dealing with notions of vagueness in #logic, that it should be no surprise that vagueness starts creeping in everywhere. For example, instead of saying that a particular logical implication is non-monotonic, we can use the logic to *define* the ordering on the underlying set of truth values (the lattice). The figure shows the "orderings" induced by the #RM3 implication (top) and the Sugihara implication (bottom) for \( n = 5 \). Here, the "arrow" on the lattice is not \( \le \). In general as \( n \) increases, only the innermost (resp. outermost) pairs of arrows remain "increasing only", for the two implications. Odd \( n \) only. Other implications are apparently "reversible", although there is the matter of what lattice values are to be considered "valid". For RM3, non-negative values are valid. Sugihara uses "not false (-2)" I think. Have to check that.

"An odd Sugihara monoid is a residuated distributive lattice-ordered commutative idempotent monoid with an order-reversing involution that fixes the monoid identity."

"A category equivalence for odd Sugihara monoids and its applications"
Galatos & Raftery (2012)

In the \( n = 3 \) case it's the same as #RM3

@andrejbauer https://www.jstor.org/stable/2275433 https://onlinelibrary.wiley.com/doi/abs/10.1002/malq.19860320106
R. Meyer et al. have written about this. It seems you need an infinity axiom, but otherwise it's OK? #RM3 can be built from the arithmetic of \( F_4 \), so it's friendly with PA, but I've only looked at finite things. Chang's MV algebras are infinitary ... I need to read more about this
https://en.wikipedia.org/wiki/MV-algebra

In case you haven't read all my other posts, lol, relevant logic is the same as paraconsistent logic, with the addition of the contrapostive. That is a paraconsistent implication doesn't satisfy the contrapositive. So what you do is define the relevant implication \( A \Rightarrow B \) as \( (A \rightarrow B) \wedge (\lnot B \rightarrow \lnot A) \) where \( A \rightarrow B \) is a paraconsistent implication. That's the major difference between paraconsistent and relevant. So RM3 is also paraconsistent.

Oh, the defining property is rejection of Weakening \[ (A \Rightarrow (B \Rightarrow A)) \]but this is, by the tensor-hom adjuntion, the projection \[ (A \otimes B) \Rightarrow A. \]It means the product isn't Cartesian. That's if you define it that way.

@ryk047 @andrejbauer

I've written some here (search for #RM3) https://mathstodon.xyz/@CubeRootOfTrue/110775995709463374 about the naturalness of RM3, it is essentially the "complex logic" you get by solving the equation \( A \wedge \lnot A = \top \), akin to \( x^2 + 1 = 0 \) in the reals. In fact it's \( x^2 + x + 1 = 0.\)

Gödel said that blah blah either inconsistent or incomplete. 20th century mathematicians were so horrified at the thought of inconsistency it's been effectively banished (the "law" of excluded middle). We're happy, apparently, with incompleteness. But what about the opposite case!? Gödel himself developed a 3-valued logic, because he obviously understood that if you allow inconsistency, you can have completeness.

Normally inconsistency can't be tolerated because \( (A \wedge \lnot A) \supset B \), you can prove anything from an inconsistency, aka the principle of explosion. Hence the horror.

In a 3-valued logic, there are statements that are inconsistent, but the logic doesn't allow explosion, so everything's under control.

So yes, #paraconsistent and #relevant #logic have very much to do with foundations.

And yes, it's possibly the simplest example of a symmetric closed monoidal category (symmetry is optional), and maybe a useful teaching tool, not to mention that it's a superior logic than 2-valued logic, as it can handle vagueness.

I should also point out that when I say there is an adjoint pair here, I'm not talking about the arrows in the poset. Usually, you would say\[
((A \otimes B) \le C) \cong (A \le (B \Rightarrow C)) \]to indicate the adjunction. But in the 4-valued case, \( B \) is not comparable to \( N \) (it's not a total order), so instead I'm writing\[
((A \otimes B) \Rightarrow C) \cong (A \Rightarrow (B \Rightarrow C)) \]
If you define \( \lnot\Diamond A \) so that \( \{ F, N \} \) are not valid and \( \{ B, T \} \) are valid, then you get the regular twist implication. But if \( N \) is not valid then the axiom \( S \) fails for both \( \Rightarrow \) and \( \Rightarrow_F \). So it's valid, but if you ask it, it'll say "I don't know."
In the logic FOUR, which can also be implemented in the algebra of \( \mathbb F_4 \), \( N \) is considered valid and\[ ((A \Rightarrow F) \vee B) \wedge ((\lnot B \Rightarrow F ) \vee \lnot A)\] is the same as \( A \Rightarrow B \), shown here:\[
\begin{array}{c|cccc}
\Rightarrow_{FOUR}&F&N&B&T\\
\hline
F&T&T&T&T\\
N&F&N&F&T\\
B&F&F&B&T\\
T&F&F&F&T
\end{array}\]In this case, \( N \Rightarrow_{FOUR} N = N \), and \( N \) is otherwise banished from the result.

All of which is to say, 4-valued logics are complex. There are several choices for the operators, differing in how they handle the 4th value and which theorems they reject. At least, it seems "I don't know" should be a valid logical statement, and is otherwise like "both true and false".

The isomorphism \( B \cong N \) in \( \mathbb F_4 \) leads to #RM3, and it seems reasonable to think of \( B \) as both "maybe" and "I don't know".

Let me repeat that "I don't know" is not only valid, you should never be afraid to say it.

Busaniche and Cignoli (2011) also describe "twist structures" where truth values are pairs of binary numbers representing "truth" and "falsity", and negation is swapping:\[ \lnot(a,b)=(b,a)\,. \]When I mentioned twist structures earlier, I restricted attention to the 3-valued case \( F=(0,1), B=(1,1), and T=(0,1) \), but of course the value \( N=(0,0) \), which may be thought of as "neither true nor false", can be used as an input to the equations and circuits I showed. However, unlike with \( \mathbb F_4 \), there is no isomorphism between \( B \) and \( N \). Here's the implication:\[
(a,b) \Rightarrow (c,d) := ((a \Rightarrow c) \wedge (d \Rightarrow b), a \wedge d)
\]where the arrows on the rhs are regular binary conditionals.\[
\begin{array}{c|cccc}
\Rightarrow&F&N&B&T\\
\hline
F&T&T&T&T\\
N&N&T&N&T\\
B&F&N&B&T\\
T&F&N&F&T
\end{array}\]This has a left adjoint \( A \otimes B := \lnot (A \Rightarrow \lnot B)\). Notice that if you ignore the \( N \) rows and columns, you get the relevant implication and conjunction of #RM3.

But we can form another adjoint pair! Notice that \( A \Rightarrow F = \lnot \Diamond A \) is the type of negation used in the paraconsistent conditional \( ( A \Rightarrow F ) \vee B \). If we "and with the contrapositive", we get an implication \( \Rightarrow \_F \) that is exactly the same, except that \( N \Rightarrow_F N \) is \( N \) instead of \( T \). It also has left adjoint \( \lnot (A \Rightarrow_F \lnot B) \).

Perhaps this question is best left to #philosophy. What is the proper value for "if I don't know, then I don't know"? It's either \( T \) or \( N \). Another question is "is \( N \) valid?" If it isn't valid, then Modus Ponens fails for \( \Rightarrow_F \).

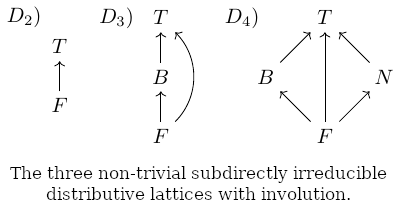
We've got a 2-valued logic, a very nice 3-valued logic called #RM3, and "A useful four-valued logic", N. D. Belnap, 1977. The obvious question is, what about \(n\)-valued logics, for \( n \ge 5 \)? Sadly, the very nice structures we've seen don't generalize. This is often the case, as when we go from the reals to the complex numbers we lose ordering, and when we go to the quaternions we lose commutativity. So it is with this family of logics. Going from 3 to 4 values breaks ordering, but enough structure remains to have something workable (and non-monotonic logics are definitely a thing). Beyond 4 though, we lose more important structure. In Kalman, J. A. (1958) "Lattices with involution," Kalman (no, not Kálmán), showed that these three, plus the trivial lattice \( D_1 \), are the only distributive lattices with involution, the involution being the negation \( \lnot \lnot A = A \). Any larger \( D_n \) decomposes into the smaller ones. Any element of a lattice that satisfies \( \lnot x=x \) is called a 'zero', and Kalman showed that for this setup, there can be only 0, 1, or 2 zeros, corresponding to the 3 lattices shown in the figure.

Furthermore there is a simple proof in Busaniche and Cignoli (2011), "Remarks on an algebraic semantics for paraconsistent Nelson’s logic," that #RM3, the \( D_3 \) lattice with involution, is *unique*.

It is still possible to construct logics with more than 4 (even infinite) truth values, but you lose monotonicity, or other nice properties. #RM3 obeys the law of small numbers; its unique structure follows from it being the *smallest*. The monoid multiplication in \( \mathbb F_4 \) contains the smallest symmetric group \( S_3 \) on 3 elements, aka the Bellman's Rule

I honestly wonder why the relevance #logic #RM3 is not taught in high school. Not only is it an obvious extension, and still relatively simple, but it works BETTER than regular binary logic!

It is a myth, by the way, that modern computers use binary logic. They don't. Deep within their electrical circuits are logical states like X for Don't Care and N for No Connection. Some have many more than 2 states.

You don't need non-binary logic everywhere! It's pretty useless in an adder, for example. Binary logic is good at stuff like that. As long as your inputs are consistent.

Where non-binary logic really comes in handy is things like the law, or politics, where disentangling the validity of assertions can be hard, because natural language is full of ambiguities and vagueness. You need a #paraconsistent logic.

One of the big paradoxes of #Logic is that there is a system of logic (intuitionistic) which rejects the law of the excluded middle, yet still manages to be a *binary* logic. You're just not allowed to use\[ \vdash P \vee\lnot P\]in proofs. You can't use double negation elimination, \(\lnot\lnot A = A, \) either.
These restrictions are claimed to make it more like a constructive proof, or something.
Well, #RM3 itself can be constructed from \( \mathbb Z_2 \) and the equation \( A \wedge \lnot A = \top \) via a field extension, negation is an involution so double negation is the identity, and the law of the excluded middle is completely valid.
Yes, that's right, \( A \vee \lnot A \) is valid in RM3. So is \( \lnot ( A \wedge \lnot A )\), unsurprisingly. Not only that, proof by contradiction works just fine.\[\begin{array}{l}
(A \Rightarrow \lnot A) \Rightarrow \lnot A \\
(A \Rightarrow (B \wedge \lnot B)) \Rightarrow \lnot A\,.
\end{array}\]Some care is needed here, though; the latter form, because it introduces a new proposition \( B, \) requires the use of the relevant implication to be valid.
It seems like RM3 satisfies the requirements one would want for constructive mathematics. A very natural, finite structure, that does everything binary logic can do and also more. It is also the answer to a question somebody learning about logic for the first time is bound to ask, "What about Maybe?"

In relevance logic, the axiom of Weakening is rejected. Since we are in a monoidal category, we can understand this as the tensor product not having projections (or rather, the projections are invalid).\[(A \Rightarrow (B \Rightarrow A)) \Leftrightarrow ((A \otimes B) \Rightarrow A).
\]
In binary logic, the quantifiers \( \forall \) and \( \exists \) can be described as being adjoint to Weakening. That is, they depend in an essential way on the projections from the conjunction existing, which they do in the ordinary Cartesian case, but not for the relevant conjunction. Of course we can still have quantifiers in #RM3 via the binary conjunction, but we also get them through the modal operators at the level of the tensor product. \( \Diamond A \) acts like \( \exists A, \) and the dual \( \square A := \lnot \Diamond \lnot A, \) necessity, acts like \( \forall. \)
For even more fun, you can define a "multimodal" logic, with more than one non-Cartesian product and associated modes. For example \( K \varphi, \) it is known that \( \varphi, \) or \( B \varphi, \) it is believed that \( \varphi. \)

#RM3 is seen to have the structure of a symmetric monoidal closed category. The ordinary conjunction and disjunction are Cartesian, but we also have a non-Cartesian tensor product that is left adjoint to the relevant implication. This structure is also described as a residuated lattice.

Symmetry is optional, and we can easily define non-commutative versions of the operators, which is done for example in the Lambek calculus model of natural language, and Linear Logic (linear here means "sequential").

RM3 is robust to paradox. The usual paradoxes of the "material conditional" fall, they are paradoxes in binary logic because the conditional there is NOT "material", it is just called that. A true material conditional, like a material witness, is a relevant conditional. Paradoxes of relevance are often called "informal" fallacies because in binary logic they are tautologies. Only the relevant implication can see them.

TL,DR; there is really only one difference between binary logic and RM3, which means that there are really two differences but they are the same. Everything else works the same way, but to avoid paradox, all you need to remember is not to do either of\[\begin{array}{l}
\phi \Rightarrow \bot \\
\top \Rightarrow \phi
\end{array}\]Both are invalid. That is, reasoning from inconsistency, or reasoning towards inconsistency, are both bad. And since at the start, we equated "Both" with "Neither", we can also say reasoning from/towards "I don't know" is just as bad.

Happy Applied #categoryTheory week.

I'm going to summarize the construction of #RM3.

Just as one can construct the complex numbers from the reals by solving the equation \( x^2 + 1 = 0 \) to get \( x = \pm\sqrt{-1}, \) we can express "A and not A is True" in Boolean Algebra as \( x (x+1)=x^2+x=1. \) The field extension \( \mathbb Z_2 / (x^2+x-1) \) creates two new truth values, \( \phi \) and \( \phi + 1 \) within the 4-element field \( \mathbb F_4, \) along with 0 and 1, so that\[\phi (\phi + 1)=1\,.\]The two new truth values are often called "Both" and "Neither," and display a symmetry (within \( \mathbb F_4 \)) such that we may ignore "Neither" and replace it with "Both" everywhere. The result is a 3-valued logic that we still need to work on a bit. Conjunction (\( \wedge \)) is multiplication, and negation (\( \lnot \)) is the involution\[\begin{array}{r|l}
A & \lnot A \\
\hline
\bot & \top \\
\phi & \phi \\
\top & \bot \\
\end{array}\]Disjunction (\( \vee \)) is the DeMorgan dual of conjunction.

Within \( \mathbb F_4 \) lurks the important operator \( \Diamond, \) the modal "possible", which serves to define the notion of validity in the logic. It is implemented by cubing.\[\Diamond A:=a^3\]This lets us define a paraconsistent implication\[A \rightarrow B := \lnot\Diamond A \vee B\]that satisfies \( A \wedge \lnot A \not\rightarrow B, \) that is, it is not explosive. We then define relevant implication as \[ A \Rightarrow B := (A \rightarrow B) \wedge (\lnot B \rightarrow \lnot A)\,. \]Finally the tensor-hom adjunction gives us the monoidal product \( \otimes \) as \( \lnot (A \Rightarrow \lnot B), \) with \( \phi \) as unit, \( \phi \otimes A = A,\) and \( \oplus \) is dual to \( \otimes. \)

Seen on \( \mathbb X: \) "Did you know the Late-Night shows have been shutdown for almost 3 months during the writers strike ... and nobody cared or missed them?"

This is how people lie with relevance fallacies. The first part of the sentence is true, while the last part is highly questionable. The "... and" makes it seem like this is a single statement, but it isn't. Phrasing it as a question makes it into an implication.\[ \begin{array}{lr}
\top \otimes \phi = \top & \\
\lnot (A \otimes \lnot B) = (A \Rightarrow B) & \text{(1)} \\
\top \Rightarrow \phi = \bot & \\
\top \rightarrow \phi = \phi & \text{(2)} \\
\end{array}\]

We model the use of conjunction with the relevant product \( \otimes \) in the #logic #RM3. Unlike with \( \wedge, \) the binary "and", conjoining statements with \( \otimes \) creates a single object that is a mixture representing both parts; \( \top \otimes A \) is not simply the identity.

From #categoryTheory and the tensor-hom adjunction we get that the monoidal product and the relevant implication are interdefinable (1). In other words saying "and" here is a sneaky way of saying "and so". It follows immediately that the entire statement is a fallacy. Note that for the paraconsistent conditional (2), the statement is still valid. It is a fallacy of relevance, which is a sort of contrapositive version of explosion, and the paraconsistent conditional doesn't see it.

Of course in the binary case this is a tautology, which is why relevance fallacies are often called "informal fallacies": the binary formalism fails to see them. But they can be treated perfectly formally, you just need a third truth value.

Of course we might not want commutativity! The contrapositive is a standard feature of binary logic, but doesn't always hold in real situations. The paraconsistent implication \( A \rightarrow B \) does not satisfy the contrapositive, but we can do it another way, too, a way we get for free from category theory.

We're touching on a larger issue here, too. Expanding our notion of #logic is great and all, but at some point we might like the syntactic machinery to correspond in a nice way to how things work in the real world. For some definition of nice. To that end having a rich set of tools is a great help, and the tensor-hom adjunction provides yet one more. Every adjunction \( L \dashv R \) induces a monad \( R \circ L \) and a comonad \( L \circ R. \) The comonad is a non-commutative product, and the monad gives us both left and right implications\[
\begin{array}{l}
A \rightharpoonup B := R_A(L_A(B) \\
A \leftharpoondown B := \lnot B \rightharpoonup \lnot A
\end{array}\]Both of these show up in the Lambek Calculus, which is used to model natural languages, and Linear Logic, where "linear" means a sequence of events. The comonad \( A \oslash B \) can be read as "B after A":\[
\begin{array}{c|ccc}
&F&B&T\\
\hline
F&F&F&F\\
B&F&B&T\\
T&F&F&T\\
\end{array}\]which allows \( \top \) after an inconsistency but not the other way around.

#RM3 is usually not presented in its full categorical glory, making it difficult at first glance to compare it with its cousins. But they are all really the same structure. Our derivation has used only universal constructions, and the monoidal closed category structure is essentially unique. There is no 4-valued version. Going to 4 breaks things. 3 is the right number.

Another consequence of the tensor-hom adjunction is that the logic has its own arrows as objects to talk about. The hom set \( [B, C] \) is called the internal hom, and is a kind of exponential object in the logical category. This is an extremely important concept in computing theory, too, where the tensor-hom adjunction is called currying, and the co-unit is called the evaluation map, eval. This is the basis of functional programming and lambda calculus.

The logic #RM3 can also talk about itself through a so-called "indicator" function, which says whether a formula is consistent or not. \( \lnot \Diamond(A \wedge \lnot A) \) is true iff \( A \) is in \( \{ \top, \bot \} \). So the logic can "know" if a formula is inconsistent or not.

For the relevant implication \( A \Rightarrow B \), we may define the adjoining tensor product as \[ A \otimes B:= \lnot (A \Rightarrow \lnot B) \]\[
\begin{array}{c|ccc}
\otimes&F&B&T\\
\hline
F&F&F&F\\
B&F&B&T\\
T&F&T&T
\end{array}\]

One of the nice things about #categoryTheory is that no matter what sort of mathematical structure you're working with, if you can match what you are studying to a particular type of known category, you instantly gain a huge trove of already-worked-out theorems about your structure. You just have to figure out what they mean.

And the same patterns keep showing up in different fields. For example, there's an entire school of #logic that uses residuated lattice theory. A residuated lattice is a lattice (a poset + some conditions) equipped with a monoidal product. That product is adjoint to the residuation operator, which is a sort of inverse for the product and plays the role of implication in logic. Categorically, it's the same structure as the relevance logic #RM3, a closed monoidal category.

The best part is what we get for free by recognizing this.

\[ (( A \otimes B ) \le C) \cong ( A \le ( B \Rightarrow C )) \]is one way to say that \( \otimes \) is left adjoint to \( \Rightarrow \). Conjunction is left adjoint to implication, as they say.

An adjunction \( L \dashv R \) is a pair of morphisms (functors) \( L: D \rightarrow C \) and \( R: C \rightarrow D \) such that there is a natural isomorphism for any \( X \rightarrow Y \): \[ (L(X) \rightarrow Y) \cong (X \rightarrow R(Y)). \]

What we get for free is that an adjunction naturally has a unit and a co-unit,\[ \begin{array}{c} \eta: X \rightarrow R(L(X)) \\ \epsilon: L(R(X)) \rightarrow X\end{array} \]and the co-unit turns out to be an especially important theorem in logic: it is modus ponens.

🧵

mix, v.: to combine, fold, or blend into one mass

A non-cartesian monoidal product \( \otimes \) in #categoryTheory is variously called "tensor", "fusion", "smash product", "and", "mix", or similar. Mix is an appropriate name for this operation, since it reflects the idea that it's irreversible. The Cartesian product \( A \times B \), another type of product available in a monoidal category, produces pairs \( (a, b), \) that can be taken apart as easily as put together.

Mix is the (relevant) conjunction in #RM3 and allows us to think logically about collections of things that become *different* when you combine them. This is where, categorically speaking, the whole is greater than the sum of its parts.

☯️

#MariaDB, the database formerly known as #MySQL, is one of the only popular computing environments on the planet to implement #paraconsistent logic. It's quite natural, of course, for a database system which accepts inputs from the real world to have a mechanism to deal with inconsistent or missing data. That mechanism is the paraconsistent logic LP.

It is thus possible to build a fully relevant #RM3 implication in an SQL Select statement. The three values of the logic are 0, 1, and None. The table t, here, is just a list of all pairs (a, b).

select a, b, (not a) or b, a is false or b,
(a is false or b) and ((not b) is false or not a) from t

a b ~a|b a->b a=>b
----------------------------------------
0 0 1 1 1
0 None 1 1 1
0 1 1 1 1
None 0 None 0 0
None None None None None
None 1 1 1 1
1 0 0 0 0
1 None None None 0
1 1 1 1 1

The last three columns show the ordinary (non-paraconsistent) conditional, the paraconsistent conditional, and the relevant conditional, resp., the latter being implemented by applying the contrapositive to the paraconsistent conditional.

Validity is expressed by "not false". This is an important concept. For the binary conditional, validity is ALSO "not false", but the lack of any other choice makes this concept invisible. Graham Priest has written extensively about this topic, and the semantics of LP.

In particular, \[ (a \wedge \lnot a) \rightarrow b \]is not valid, because None -> 0 is false, and your database won't explode when it hits a None.

Note to the geeks out there who want to add some robustness to their databases: you can usually create a function in SQL like Imp(a, b) or something, so you don't have to constantly write the whole expression out every time.

Speaking of transitivity,\[
((F \Rightarrow B) \wedge (B \Rightarrow T)) \Rightarrow (F \Rightarrow T) \]is valid in #RM3, and along with the identities \( a \Rightarrow a \) (all valid) makes \( \{ F, B, T \} \) into a category, a poset, with the arrows given by \( \Rightarrow \). This is then valid:\[ (a \Rightarrow b) \Rightarrow (a \le b). \]Am I doing something fishy there with that middle arrow? Not really, it's still valid if I use \( \rightarrow \). But \[ (a \rightarrow b) \not\Rightarrow (a \le b). \]The lack of contrapositivity makes it non-monotonic. But wait. Is it *really* not fishy? I appear to be using a formal, syntactic implication to represent a semantic relationship.

Hmm.
#categorytheory

OK, so for #RM3, we're going to do a couple things. First, we'll stick with T, B, and F as truth values. Then in the addition and multiplication tables, we ignore the N rows and columns, and change all the remaining Ns into Bs. Multiplication is AND. Addition is XOR. And NOT has the nice property that \( \lnot \lnot a = a \) (it's idempotent).

NOT\((a)\) is \( a + T \).
\[
\begin{array}{c|c}
a & \lnot a \\
\hline
F & T \\
B & B \\
T & F \\
\end{array}\]\[
\begin{array}{c|ccc}
\wedge & F & B & T \\
\hline
F & F & F & F \\
B & F & B & B \\
T & F & B & T \\
\end{array}\]Inclusive OR is defined by DeMorgan duality:\[
\begin{array}{c|ccc}
\vee & F & B & T \\
\hline
F & F & B & T \\
B & B & B & T \\
T & T & T & T \\
\end{array}\]and the regular conditional \(\lnot a \vee b \):\[
\begin{array}{c|ccc}
\supset & F & B & T \\
\hline
F & T & T & T \\
B & B & B & T \\
T & F & B & T \\
\end{array}\]
At this point, we have a basic 3-valued logic. We aren't where we want to be yet, though. This logic is still explosive. The conditional is too weak. This is because we have expanded our notion of Truth. Things are no longer black or white.

The conditional is defined as "NOT a OR b". But is it appropriate to use the ordinary negation? \( \lnot B = B \), so are we negating anything?

Instead of Truth, we need to think in terms of Validity. In #RM3, both T and B are "designated" as valid. So our conditional should be \[ a \rightarrow b =_{def} \lnot \text{valid}(a) \vee b. \]And it turns out that there is a natural way to implement valid\(a\).