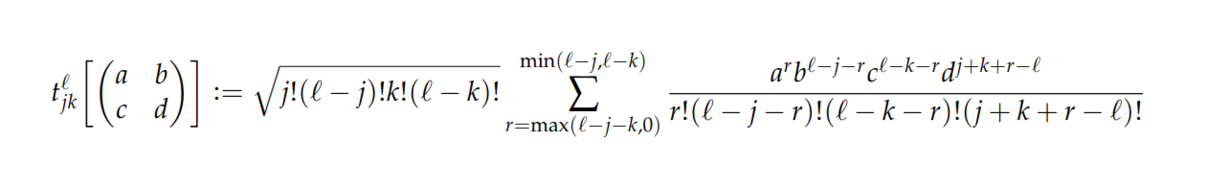This week I posted a paper which I basically wrote during my first couple years of graduate school to the arXiv. You can find the preprint "A partition formula from idempotents" at https://arxiv.org/abs/2308.10177.

I feel a bit conflicted about this paper. Even after posting it I'm not sure how interesting it is. I showed the formula obtained therein to several people, including my advisor, while I was in grad school and people seemed generally unsure what to make of it.

Partition numbers are not something I ever studied much. My impression is that there is neither a known elementary formula nor a proof that one cannot exist. I'm not even sure if there is a rigorous, accepted definition of what would constitute a closed-form elementary formula in this context, since lots of fun can be had in summing over neat sets as in this paper.

#combinatorics #RepresentationTheory #AbstractAlgebra #algebra #NumberTheory

I am working my way through Adams's "Lectures on Exceptional Lie Groups", and I am not satisfied with the proof for his proposition 4.2 (which states the even subalgebra for the Clifford Algebra \(Cl(V)_{0}\) has 1 irreducible representation when \(dim(V)=m=2n+1\) and 2 irreducible representations when \(dim(V)=m=2n\) with certain specific weights).

The argument seems to be to relate representations of an Abelian subgroup \(E=\{\prod^{m}_{j=1}e_{j}^{i_{j}}\mid i_{j}=0\mbox{ or }1\}\) and \(E_{0} = E\cap Cl(V)_{0}\) [where \(e_{j}\) form the canonical basis for \(V\)] to representations of \(\mathbb{R}[E]/(\nu + 1)\cong Cl(V)\), the quotient of the group algebra \(\mathbb{R}[E]\) modulo the identification of the square of the generators \(e_{j}^{2}=\nu\) with -1.

I'm with Adams until he picks a complex 1-dimensional representation \(W\) of \(F\), because he starts working with *COMPLEX* representations. But Adams triumphantly announces "We thus get a representation, \(\Delta\) of \(E_{0}\)..." then shows it is irreducible. I'm fine with it being irreducible from the character relations, that's fine.

Even supposing this is an irreducible representation for \(\mathbb{C}[E_{0}]\), I don't quite see how to obtain an irrep for \(Cl(V)_{0}\); I am guessing just extend it "in the obvious way"? Does this preserve irreducibility?

#RepresentationTheory #LieGroups #CliffordAlgebra #Mathematics #Proof

Quiver algebras have the property that, in any fixed dim, rep(Q) is a vector space. Is there some characterization of which algebras have this property?

(Unital algebras seem to be ruled out. Except kQ *is* unital, but for those you can just "throw away" the 1, and all the primitive idempotents in fact, and it works. I guess it's because they have an k-linear decomposition \(kQ = E \oplus I\) where E is the subalgebra of idempotents and I is an ideal, and any representation of Q is uniquely determined by what it does on I (which is a non-unital subalgebra), since it has no choice of what to do on E. Not quite sure what the right general principle is here though...)

#RepresentationTheory #quivers

Anyone know the tame/wild classification for finite *cyclic* quivers? The oft-quoted one is for acyclic.

I can see any quiver w/ two cycles is wild, and any graph that is just one cycle is tame. Having trouble finding anything written about classifying other unicyclic quivers.

#RepresentationTheory #quivers #wild

#groups #RepresentationTheory #LieGroups

As a kid, I was a lazy programmer and would often get off by one error in loops. If only I knew about Weyl vector then 😁
#coding #RepresentationTheory

Well, lol. There we go. #RepresentationTheory :p
It's time to solve my exercises, lol.

While it may look ugly (or scary) to you, I think this is one of the most beautiful formulas in #RepresentationTheory. It is an explicit formula for any #representation of a 2 x 2 matrix. It lets you increase a 2 x 2 matrix to any size you want, while still miraculously preserving matrix multiplication!

It was first derived by Wigner and is known in physics as Wigner D-matrix.
https://en.wikipedia.org/wiki/Wigner_D-matrix

Appendix C of our paper has a great introduction to #RepresentationTheory of 2 x 2 matrices. If you ever wanted to learn this stuff, I recommend you have a look!

Here is how the first few representations look like. While it's not obvious, these maps are homomorphisms from 2 x 2 matrices to d x d matrices, and there exists one such map for every dimension d!

Hello all! I'm a PhD student studying #RepresentationTheory and #LieTheory . My other interests are in programming (especially in #Julia ) and dancing. If you're interested in any of these topics (or anything tbh), feel free to chat in DMs.

This is me hopping on the Mastodon ~train~ elephant and my #introduction.