Jon Awbrey · @Inquiry
152 followers · 764 posts · Server mathstodon.xyzJon Awbrey · @Inquiry
137 followers · 644 posts · Server mathstodon.xyz#RiffsAndRotes • Happy New Year #2023
• https://inquiryintoinquiry.com/2023/01/01/riffs-and-rotes-happy-new-year-2023/
Let \(p_n\) = the \(n^\text{th}~\text{prime}.\)
Then \(2023=7\cdot{17}^2=p_{4}p_{7}^2=p_{{p_1}^{p_1}}p_{{p_4}}^{p_1}=p_{{p_1}^{p_1}} p_{{p_{{p_1}^{p_1}}}}^{p_1}\)
No information is lost by dropping the terminal 1s. Thus we may write the following form.
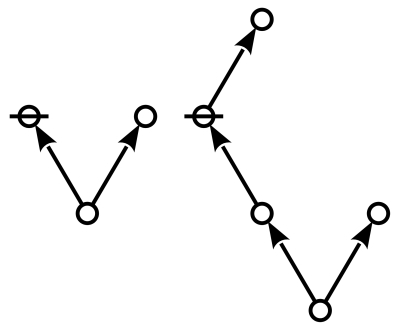
\[2023=p_{p^p} p_{{p_{p^p}}}^p\]
Forms like these correspond to a family of #Digraphs called #Riffs and a family of #Graphs called #Rotes.
#primes #numbertheory #graphtheory #rotes #graphs #riffs #digraphs #RiffsAndRotes
Jon Awbrey · @Inquiry
135 followers · 638 posts · Server mathstodon.xyz#RiffsAndRotes • Happy New Year 2023
• https://inquiryintoinquiry.com/2023/01/01/riffs-and-rotes-happy-new-year-2023/
\(2023 = 7 \cdot {17}^2 = p_4 p_7^2 = p_{p_1^{p_1}} p_{p_4}^{p_1} = p_{p_1^{p_1}} p_{p_{p_1^{p_1}}}^{p_1}\)
Jon Awbrey · @Inquiry
94 followers · 373 posts · Server mathstodon.xyzJon Awbrey · @Inquiry
94 followers · 373 posts · Server mathstodon.xyz
Jon Awbrey · @Inquiry
74 followers · 247 posts · Server mathstodon.xyz#Riffs from 1 to 60
• https://oeis.org/w/images/1/17/Animation_Riff_60_x_0.16.gif
#Rotes from 1 to 60
• https://oeis.org/w/images/e/ee/Animation_Rote_60_x_0.16.gif
Jon Awbrey · @Inquiry
34 followers · 119 posts · Server mathstodon.xyzJon Awbrey · @Inquiry
22 followers · 51 posts · Server mathstodon.xyz• https://oeis.org/wiki/Riffs_and_Rotes
#Arithmetization #GödelNumbering
#DoublyRecursiveFactorization #DRF
#Arithmetic #NumberTheory #GraphTheory
#PrimesFactorization #PrimeNumbers #Primes
#primes #primenumbers #PrimesFactorization #graphtheory #numbertheory #arithmetic #DRF #DoublyRecursiveFactorization #GödelNumbering #Arithmetization #RiffsAndRotes