The spectre (and friends): aperiodic monotiles *without reflection*

This is very cool! 😎

https://vm.tiktok.com/ZGJxCtuWM/

#mathematics #RecreationalMathematics #tiling #tesselation #AperiodicTiling

a new #monotile was discovered that allows for #aperiodictiling of the plane. I made a short tutorial that explains how to model the #einstein to play around with it in blender and puzzle around without having to 3d print it

#tessellation #tiling #aperiodic #modeling #b3d #blender3d

https://www.youtube.com/watch?v=TnE2PK5n8Ww

Finally got a chance to read the big math news this week on #AperiodicTiling discovery. PAPER: https://arxiv.org/pdf/2303.10798.pdf Looking forward to hearing more at special Gathering4Gardner Sunday 9am PDT @g4gcelebration@twitter.com

An aperiodic monotile, https://arxiv.org/abs/2303.10798.

This is so awesome.

#tiling #AperiodicTiling #polyform

@csk #AperiodicTiling

Wow!! What a breathe of fresh air this paper is in the midst of suffocating levels of "AI solves everything" hype cycle.

https://arxiv.org/abs/2303.10798

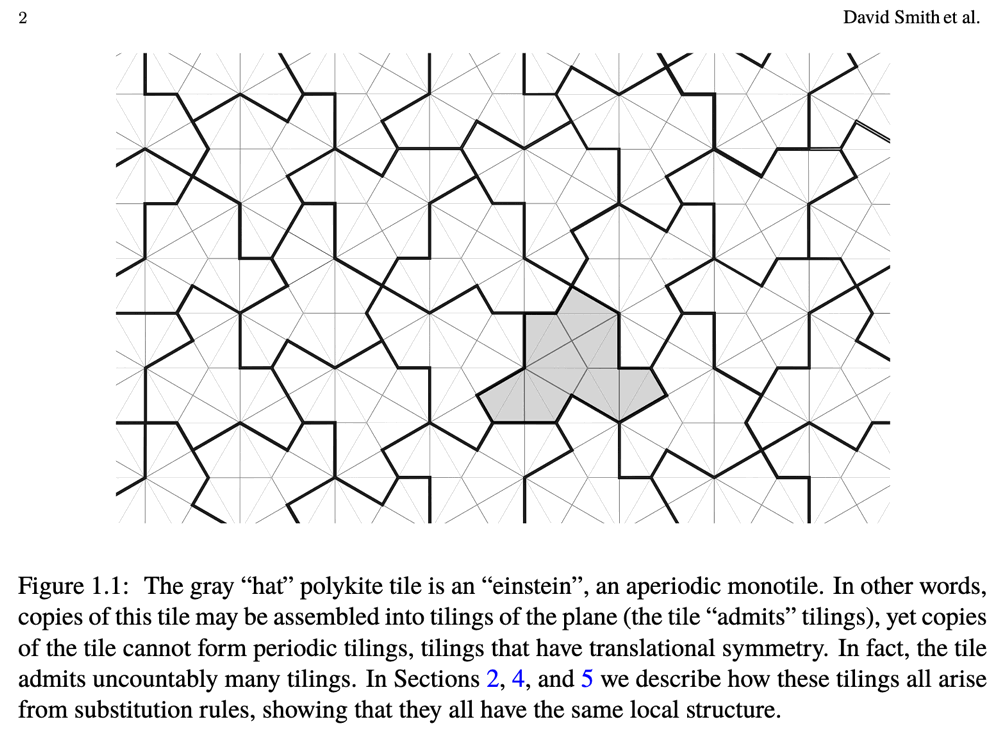
They have found at long last, a single tile, an "einstein", which they call a "hat"/polykite that tiles the entire plane aperiodically.

Previously the best known aperiodic tiling of the plane required at the least two different tiles, the most famous ones being the Penrose tiles, and those that adorn Alhambra.

It is all the more wonderful that the first two authors don't have any academic/research affiliations. They write somewhere in the paper, how it all started, so wonderful:

"One of the authors (Smith) began investigating the hat polykite as part of his open-ended visual exploration of shapes and their tiling properties. Working largely by hand, with the
assistance of Scherphuis’s PolyForm Puzzle Solver software (www.jaapsch.net/puzzles/
polysolver.htm), he could find no obvious barriers to the construction of large patches, and yet no clear cluster of tiles that filled the plane periodically."

Why is the study of tilings such a big deal? Well, it hints at and tries to formalize various physics concepts that are of immense interest to many of us (and dare I say, even neuroscientists): quasi crystals!, possible new states of matter, emergent structures from simple units, how symmetries and asymmetries arise, stability of heterogenous media, soft matter physics, order without periodicity, criticality etc., etc.,

On quasi-crystals and their search, applications, uses etc., I recommend the wonderful Paul Steinhardt's book: "The Second Kind of Impossible: The Extraordinary Quest for a New Form of Matter"

#Physics #Maths #Combinatorics #AperiodicTiling #PenroseTiles #Einstein #Emergence #condensedmatter