#DifferentialPropositionalCalculus • 6.2
• https://inquiryintoinquiry.com/2020/03/02/differential-propositional-calculus-6/

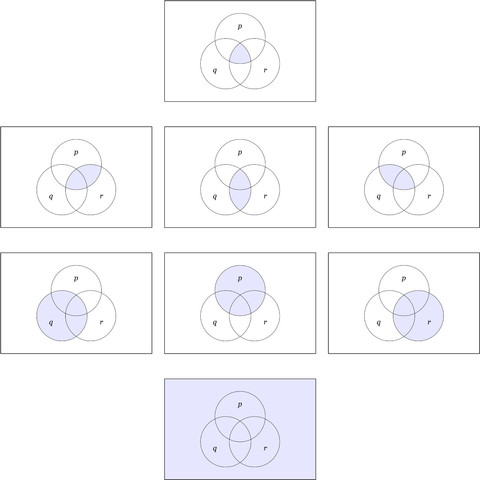
Figure 9. #VennDiagrams for the #PositivePropositions on 3 Variables
• https://inquiryintoinquiry.files.wordpress.com/2020/03/venn-diagrams-e280a2-p-q-r-e280a2-positive-propositions.jpg

Rank 3 (Top). #VennDiagram for the #BooleanProduct or #LogicalConjunction \(pqr.\)

Rank 2. Venn Diagrams for the 3 #BooleanProducts \(pr,\) \(qr,\) \(pq.\)

Rank 1. Venn Diagrams for the 3 #BasicPropositions \(p,\) \(q,\) \(r.\)

Rank 0 (Bottom). Venn Diagram for the #ConstantFunction or the #ConstantProposition \(1.\)

#DifferentialPropositionalCalculus • 5.5
• https://inquiryintoinquiry.com/2020/02/29/differential-propositional-calculus-5/

The third row of Figure 8 shows #VennDiagrams for the 3 #LinearPropositions of rank 1, which are none other than the 3 #BasicPropositions, \(p, q, r.\)

For example —

\(\text{Figure 8.3. Venn Diagram for}~p\)
• https://inquiryintoinquiry.files.wordpress.com/2020/02/venn-diagram-e280a2-p-q-r-e280a2-p.jpg

Related Subjects —
#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions\)

#DifferentialPropositionalCalculus • 4.11
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

Linearity, Positivity, Singularity are relative to the basis \(\mathcal{A}.\) #SingularPropositions on one basis do not remain so if new features are added to the basis. A #BasisChange even within the same pairwise options \(\{a_i\}\cup\{\texttt{(}a_i\texttt{)}\}\) changes the sets of #LinearPropositions & #PositivePropositions as both are decided by the choice of #BasicPropositions, in effect choosing a cell as origin.

#Logic

#DifferentialPropositionalCalculus • 4.10
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

The #BasicPropositions \(a_i : \mathbb{B}^n \to \mathbb{B}\) are both linear and positive. So these two kinds of propositions, the linear and the positive, may be viewed as two different ways of generalizing the class of basic propositions.

Related Subjects —
#CoordinatePropositions #SimplePropositions
# LinearPropositions #SingularPropositions

#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions

#DifferentialPropositionalCalculus • 4.2
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

The full set of propositions \(f : A \to \mathbb{B}\) contains a number of smaller classes deserving of special attention.

A #BasicProposition in the universe of discourse \([a_1, \ldots, a_n]\) is one of the propositions in the set \(\{a_1, \ldots, a_n\}.\) There are of course exactly \(n\) of these. Depending on the context, #BasicPropositions may also be called CoordinatePropositions or #SimplePropositions.

#LogicalGraphs