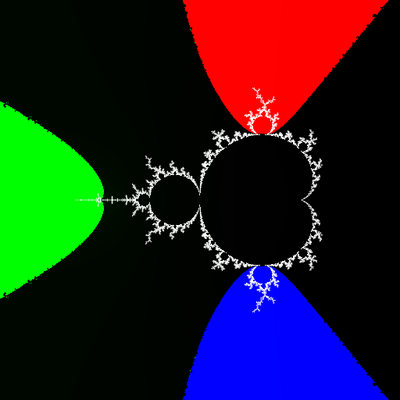
claude · @mathr
288 followers · 2739 posts · Server post.lurk.orgFigured out how to plot wakes implicitly.
Given a wake with parameter ray angles $s_-, s_+$, for each pixel $c$ in the image trace the dynamic rays at those angles towards the Julia set: if and only if they land together, then $c$ is in the wake.
An application of Theorem 2.5 from https://arxiv.org/abs/1709.09869 "A survey on MLC, Rigidity and related topics" by Anna Miriam Benini.
Previously I had been tracing the two parameter rays into a polygonal boundary and filling that using rasterization, to do: benchmark and compare the two methods in various scenarios.
#MandelbrotSet #JuliaSet #fractal #maths #ComplexDynamics #ExternalRays
#externalrays #ComplexDynamics #maths #fractal #juliaset #MandelbrotSet
claude · @mathr
288 followers · 2739 posts · Server post.lurk.orgIf I read this right, different angles landing on the same point can have different Hubbard trees? This seems counterintuitive.
37/224 lands with 39/224, 43/224 but is in (1/7, 39/224)
claude · @mathr
288 followers · 2739 posts · Server post.lurk.orghttps://arxiv.org/abs/1911.03796 #amreading #maths #MandelbrotSet #ExternalRays
A formula to transform rays from hyperbolic components to the real axis.
New to me terminology:
- vein (not exactly sure what this is, paper needs more diagrams and examples in binary instead of decimal)
- pseudocentre (tip of ray pair or vein)
- complexity (length of binary expansion of dyadic rational / pseudocentre / vein)
- kokopelli component (upper period 4 island)
- maximally diverse sequence
#amreading #maths #MandelbrotSet #externalrays
claude · @mathr
288 followers · 2739 posts · Server post.lurk.orgOrdering rays to see how to construct the tip rays (one letter inside ()) from their neighbouring hub rays (five letters inside ()).
```
. O(o) -- one lo
. O(o o o o i)
.(O) -- central lo
.(I) -- central hi
. I o o o o(i) -- five lo
. I o o o i(o) -- five hi
. I(o o o i o)
. I o o o(i) -- four lo
. I o o i(o) -- four hi
. I(o o i o o)
. I o o(i) -- three lo
. I o i(o) -- three hi
. I(o i o o o)
. I o(i) -- two lo
. I i(o) -- two hi
. I(i o o o o)
. I(i) -- one hi
```
The pattern seems to be "match longest prefix of neighbouring hub rays, then append o(i) and i(o). Except for spoke five. Needs to be verified for other locations, just in case it is a fluke.
This is reminiscent of my 2013 blog posts about #ExternalRays in the #Mandelbrot set:
navigating by spokes: https://mathr.co.uk/blog/2013-02-01_navigating_by_spokes_in_the_mandelbrot_set.html
> The tip of each spoke is the longest matching prefix of neighbouring angles, with 1 appended.
islands in the hairs:
https://mathr.co.uk/blog/2013-10-02_islands_in_the_hairs.html
> Actually, a finite binary expansion is really an infinite binary expansion, ending in an infinite string of 0s. But there's another infinite binary expansion for each number ending in infinite 0s, that ends in an infinite string of 1s: .xyz1000... = .xyz0111...
By the tuning algorithm 1(0) and 0(1) become i(o) and o(i), I suppose.
claude · @mathr
288 followers · 2739 posts · Server post.lurk.orgCurrently investigating #ExternalRays in #EmbeddedJuliaSets in the #Mandelbrot set. Have rediscovered (I had forgotten) that the complex dynamics of a pre-periodic #Misiurewicz point under z→z²+c don't necessarily exactly match the dynamics of its rays under angle doubling (but there is a relationship).
For example: take an embedded Julia set with 5-fold hubs, with an influencing island of period 3. Then the main tips of the EJS where two rays land have period 3 (both point and rays), but the hubs with five spokes have period 3 in complex dynamics, but period 15 = 3 × 5 in ray dynamics.
What I'm doing now is tracing some of the rays to calculate their binary expansions, to see how they are made up from the blocks of digits from the influencing island and central island.
Later I want to see how the external angles are related when moving about inside the structure of an embedded Julia set in different ways.
#externalrays #embeddedjuliasets #mandelbrot #misiurewicz
claude · @mathr
288 followers · 2739 posts · Server post.lurk.orgI was fed up with tracing high period #ExternalRays in the #Mandelbrot set being so excruciatingly slow, so I implemented a variation using perturbation calculations.
It only works when tracing outwards from near a mini-set, not tracing inwards from infinity, and it isn't asymptotically faster, and it can't trace from deeper than 1e-300 yet as I used double instead of long double, but a large constant factor improvement is nice.