This is the fifth and final post in a series arising from the Fibonacci cusps of Kleinian double-cusp groups.

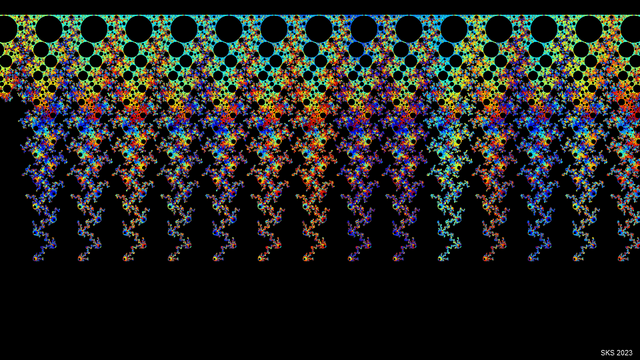
The art for this post is an ε-descent movie of the Golden Mean Group's Jorgensen projection. Unlike the other ε-descent movies, this one goes deep into the subpixel range, from 2px down to 0.01px (that is, 200x finer required granularity than the other ones). And it's clear that it's far from done revealing visible features.

Notice how you can still follow the downward paths as they trace out the Fibonacci sequence with their hairpin turns: 1-1-2-3-5 etc, but this time there isn't a final value where they will flatten out and join one another

The entire 150-frame movie took about 10 days to render; the initial frames took about 8 seconds apiece when ε~2. The final three frames, at ε~{1.012, 1.011, 101} took {24h, 28h30m, 36h) to render : over 40% of the total rendering time!

This is an example of malicious compliance by a mathematical object: it is associated with a point on the Maskit Curve, so its features do have to shrink as you descend the tree. And in the limit it will converge on being constructed entirely out of completed tangent circles, and those emergent circles will close, but it's going to take literally as long as possible to get there.

There are infinitely many other such irrational groups along the Maskit Curve which I, following the example of Pythagoras, will proceed to disregard in favor of the far-more-tractable rationals.

End of thread.

Traversal in R, rendering using Cairo, movie conversion with ffmpeg.

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #mathart #fibonacci #mastoart

#fibonaccicusps

This is the fourth in a series of posts arising from the Fibonacci cusps of Kleinian double-cusp groups.

The last post asked "why does the Golden Mean group clearly have more visible features to reveal when rendered at ε=1/40px, while the Fibonacci cusps that converge to it are done showing new visible features when ε gets down to about 2 pixels?" (see https://mathstodon.xyz/@KleinianArborist/110685414981687380)

The attached video shows an ANALOGY for the difference between "rational" vs "irrational" numbers on the Maskit curve (longer version: https://youtu.be/9FvB8WWlYPY).

It shows side-by-side renders of the first few Fibonacci cusps (Unit Circle projection) as their required granularity decreases (the bar in the middle visually displays the value of ε).

On the right the "emergent circles" close immediately, whereas on the left they never quite meet. Circles happen when an infinite word in the group has the property of "parabolicity".

All the parabolic words for double-cusp groups are predictable and repeating (by analogy, rational numbers always repeat their digits). The groups corresponding to irrational numbers also have an infinite number of parabolic words, but they're not predictable.

The image on the right has these "special words" included in the ordered list of points for each node, the left does not. Those special words make the emergent circles.

Traversal in R, rendering using Cairo, image editing in gimp.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms
#mathematicalart #generative #generativeart #mathart #fibonacci
#fibonaccicusps

This is the third in a series of posts arising from the Fibonacci cusps of Kleinian double-cusp groups.

As previously discussed, a series of fractions Fib(n)/Fib(n+1) will tend towards 1/ϕ over time. Correspondingly, the sequence of Fibonacci cusps on the Maskit curve will converge to the point corresponding to 1/ϕ, which generates what I suppose might be called the Golden Mean Group.

The μ parameter for this group for the Maskit slice where the second and fourth generators are parabolic ("tb=2") is provided in [1], specifically μ=1.2943265032+1.6168866453i (there is a mirror group with essentially the same properties at μ=0.7056734968+1.6168866453i). Curt McMullen and Troels Jorgensen were major proximate contributors to nailing this down.

Attached are Maskit and Jorgensen renders of the Golden Mean group. Interestingly, this set doesn't meet up like the Fib cusps that led up to it, even though the value of ε was set extremely low It looks like one of the intermediate frames from the walk animations, not a proper group. But what there still seems to be made up of tangent circles. What's going on? We'll start to explore that in the next post.

A completely different take on rendering this group is found in [1], fig 10.4 which is definitely worth a look if you're interested..

Traversal in R, rendering using Cairo, image editing in gimp.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #generative #generativeart #mathart #fibonacci #fibonaccicusps

This is the second in a series of posts arising from the Fibonacci cusps of Kleinian double-cusp groups.

One of the more endearing properties of the double-cusp groups is that they don't hold anything back; once you know how, you can read which group they are right off the image.

Remember how last post we were imagining jumping further and further down to the next Fibonacci cusp (1/1, 1/2, 2/3,3/5...), switching directions each time? Well, let's take a look and see what the groups themselves are telling us.

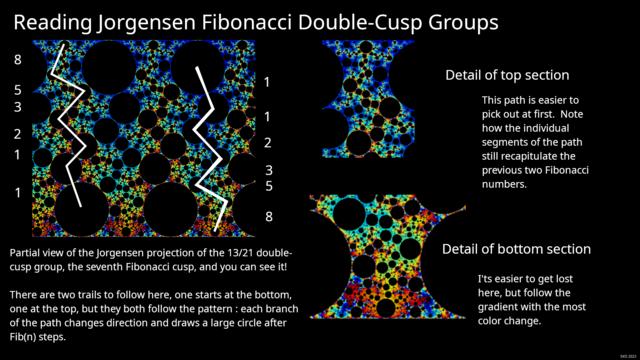
The attached image contains a selection from the Jorgensen projection of the 13/21 cusp, with a couple of paths marked through the set. If you compare to the animations in the previous post, you'll recognize the downward-tracing path as the one that's "always there". while the upward-tracing path is the one that "emerges" as you land exactly on the double-cusp point.

Note that the fractal repeats itself horizontally, so you can use the extra copy of each path in the image to follow the trace; for the later parts of the path, refer to the detail images on the right.

Pretty slick that our mental model of jumping left and right from cusp to cusp along higher and higher fibonacci counts has resulted in an image that does the same thing! Almost as though that metaphor was chosen for just that reason...

Traversal in R, rendering using Cairo, image editing in gimp.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #generative #generativeart #mathart #fibonacci #fibonaccicusps

This is the first in a serious of posts arising from the Fibonacci cusps of Kleinian double-cusp groups.

The attached static image is an illustration of the Maskit slice; if you draw a line along the topmost points in this plot, it cuts the plane into two regions: above it groups are discrete (and, among other things, are amenable to the ε-termination tool from last time), below it most groups are chaotic (plotted points being the exceptions).

Each point on the Maskit curve itself corresponds to a point on the real line between 0 and 1, inclusive; by convention we refer to those points that correspond to rational numbers "cusps"; they not only literally stand out from the curve, but also generate very appealing images made up entirely of tangent circles. But there are ofc infinitely more points that correspond to irrational numbers.

If you imagine perching on the top-right hand side spot at 2+2i, then jumping down and to the left to the next prominent cusp, then down and to the right, then left again, you'll visit:

1/1, 1/2, 2/3, 3/5, 5/8. 8/13 ...

These are the Fibonacci cusps, if you follow the path forever, it implies that you'll eventually converge on the point associated with 1/ϕ.

Art tax: Jorgensen and Maskit projections going through the first seven Fibonacci cusps and back.

[1] Mumford, D., Series, C., & Wright, D. (2002). Indra's Pearls: The Vision of Felix Klein. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107050051

[2] image credit : Curtis McMullin's web page at https://people.math.harvard.edu/~ctm/gallery/teich/maskit.gif

[3] https://en.wikipedia.org/wiki/Bers_slice

#kleinianlimitset #kleiniangroup #fractals #mobius #mobiustransforms #mathematicalart #generative #generativeart #mathart #fibonacci #fibonaccicusps