It is remarkable that the equation | x^2 | = 2 has no rational solution. But it has a solution in a finite field. I think the old Pythagorean would like the result. Today's mathematics faculties probably don't attach any further importance to the result.

#MathDay #BasicResearch #gimps #ChatGPT #OESI (41/n)

Here is the way I found this sequence independent from the handbook. Order the numbers in the Galois field G(p) symmetrically to zero. One half is denoted as positive numbers, the other as negative. If a is a positive number in this field, then the equation
| x^2 | = a has always a solution if p is a Sophie Germain prime.

Details can be found in my essay, will be published if time permits it.

#MathDay #BasicResearch #gimps #ChatGPT #OESI (40/n)

p is prime and 2p+1 is also prime. I just learned from the "The Handbook of Integer Sequences" ( https://oeis.org ) these are Sophie Germain primes.

#MathDay #BasicResearch #gimps #ChatGPT #OESI (39/n)

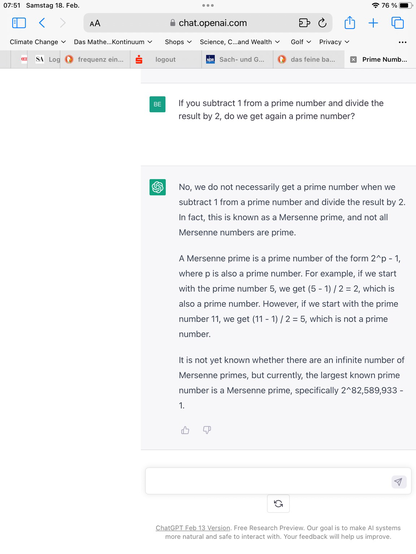
This is false and subtile misleading. Since it can be shown that for a Mersenne Prime (p-1)/2 is not a prime number. But the first million primes contain 44842 prime numbers p such that (p-1)/2 is also a prime number. For example are p=15485543 and (p-1)/2=7742771 both prime. Are there infinitely many?

#MathDay #BasicResearch #gimps #ChatGPT (38/n)

ChatGPT suggested that this question is related to the question of the existence of Mersenne Primes.

#BasicResearch #GIMPs #ChatGPT (37/n)

I am currently writing an essay which discusses the question, if the extension of the natural numbers to the real numbers unavoidable in obtaining a number system which is strong enough to formulate physical theories (like the theory of relativity and quantum mechanics). I came across the question, weather with a prime number p the number (p-1)/2 is also a prime number.

#BasicResearch #GIMPs #ChatGPT (36/n)

Happy #FullCoverageFriday, Friday the 13th edition! Watch out for #Shiny #Rubber #Gimps crossing your path! #Hypno

@objectC Heeh! Function over form. #Gimps need handles! ;)

Happy #FullCoverageFriday! Be sure and keep your #Rubber #Gimps warm in this cold weather. Maybe some #hypno to keep them relaxed and blank. ;)

Hello, can we help you with something? 😏

With @Latonex

#Rubber #Latex #Gimps #Couple #Gimp #Studiogum #Gasmask #Hood