These observations of conserved homologous expression are easy to reproduce! Go to a gene page, click "orthologs", and chose a taxonomic level, here Theria:
TLK1 https://bgee.org/gene/ENSG00000198586/#orthologs -> https://bgee.org/analysis/expr-comparison?data=4a7fc4f9fba1b1e63c458881a6ca8f5b61367fd2
HAT1 https://bgee.org/analysis/expr-comparison?data=d9510c624d21931605aa16a7c378f8ede9ce4fe6
#bioinformatics #biocuration #evodevo #ortholog #homology

'Outlier-Robust Subsampling Techniques for Persistent Homology', by Bernadette J. Stolz.

http://jmlr.org/papers/v24/21-1526.html

#homology #outliers #topological

'Intrinsic Persistent Homology via Density-based Metric Learning', by Ximena Fernández, Eugenio Borghini, Gabriel Mindlin, Pablo Groisman.

http://jmlr.org/papers/v24/21-1044.html

#manifold #homology #topological

Little request - I want to follow #homology folks here
any pointers?

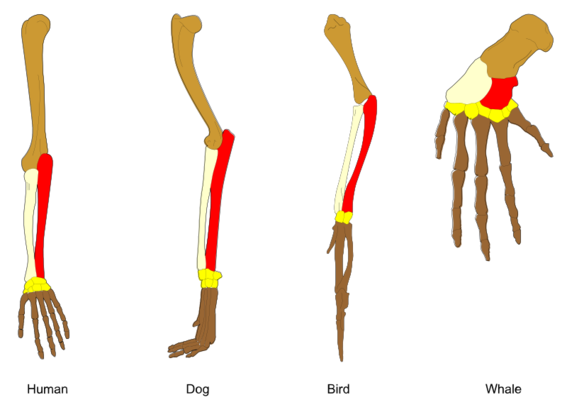
#DidYouKnow: In biology, #Homology is similarity due to shared ancestry between a pair of structures or genes in different taxa.

A common example of homologous structures is the forelimbs of vertebrates, where the wings of bats and birds, the arms of primates, the front flippers of whales and the forelegs of four-legged vertebrates like dogs and crocodiles are all derived from the same ancestral tetrapod structure.

https://knowledgezone.co.in/kbits/63030b3ccdab15e41dd0aa7d

Two p-cycles a and b are "homologous" (i.e. belong to the same #Homology class) if there exists a (p+1)-chain c, such that b = a + ∂c (mod-2 sum)
👇
https://arxiv.org/abs/2206.13932
#TopologicalDataAnalysis #TopologyToolKit #PersistentHomology #Visualization #DataScience #MachineLearning

So I was reading about n-dimensional pseudomanifold the other day (part of intro to Homology) and apparently (b),(c) here imply that the space is a strongly connected and non-branching complex. The book doesn't introduce these terms. What exactly do they mean here in this context? #homology #algebraictoplogy

Also tbh, it's a bit hard to realize what exactly this is apart from a topological space that satisfies some conditions. 😢

#Matroid s are a specific kind of sets that contain other sets, but for any set they contain, they also need to contain its subsets. For more look here:

https://en.wikipedia.org/wiki/Matroid

Looking oddly specific, they're in fact an interesting structure which pops out in the study of many combinatorial subjects like graph theory, and, as I just learned, #homology!

Well, actually, it’s a bit annoying that \(\delta\) returns lots of n-1 simplices for any n-simplex: it is a multifunction. If we instead map the other way around, from the boundary to the inside, we simply get a function! And that’s called cohomology, and is what the cool kids do all the time!

4/end

#homology #cohomology