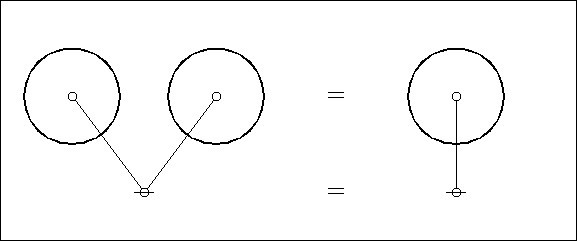Jon Awbrey · @Inquiry
109 followers · 499 posts · Server mathstodon.xyz#LogicalGraphs • 16
• https://oeis.org/w/index.php?title=Logical_Graphs&stable=0&redirect=no#Duality
#Duality • Logical and Topological
Turning now to the #InitialEquation or #LogicalAxiom whose text expression is \(\texttt{(}~\texttt{)(}~\texttt{)}=\texttt{(}~\texttt{)}\), Figure 8 shows the planar maps and their #DualGraphs superimposed.
Figure 8
• https://oeis.org/w/images/0/09/Logical_Graph_Figure_8_Visible_Frame.jpg
#Logic #Peirce #SpencerBrown #LawsOfForm
#PropositionalCalculus #BooleanFunctions
#GraphTheory #ModelTheory #ProofTheory
#ProofTheory #modeltheory #graphtheory #BooleanFunctions #PropositionalCalculus #lawsofform #spencerbrown #Peirce #logic #dualgraphs #logicalaxiom #initialequation #duality #LogicalGraphs
Jon Awbrey · @Inquiry
100 followers · 428 posts · Server mathstodon.xyz#LogicalGraphs • 15
• https://oeis.org/w/index.php?title=Logical_Graphs&stable=0&redirect=no#Duality
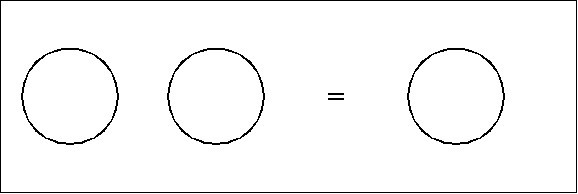
We have treated in some detail various forms of the #InitialEquation or #LogicalAxiom whose text expression is \(``\texttt{((}~\texttt{))}~=~".\) For comparison, let's record the plane-embedded & #TopologicalDual forms of the axiom whose text expression is \(``\texttt{(}~\texttt{)(}~\texttt{)}=\texttt{(}~\texttt{)}".\)
Figure 7 reproduces the planar form of the equation we first saw in Figure 1.
Figure 7
• https://oeis.org/w/images/b/b4/Logical_Graph_Figure_7_Visible_Frame.jpg
#Peirce #logic #topologicaldual #logicalaxiom #initialequation #LogicalGraphs
Jon Awbrey · @Inquiry
86 followers · 302 posts · Server mathstodon.xyz#AllLiarNoParadox
• https://inquiryintoinquiry.com/2015/08/01/all-liar-no-paradox/
A statement \(S_0\) asserts that a statement \(S_1\) is a statement that \(S_1\) is false.
The statement \(S_0\) violates an #AxiomOfLogic, so it doesn’t really matter whether the #OstensibleStatement \(S_1,\) the so-called #Liar, really is a statement or has a #TruthValue.
#Logic #LogicalAxiom #LawOfLogic #LogicalGraph
#LiarParadox #Epimenides #EpimenidesParadox
#epimenidesparadox #Epimenides #LiarParadox #logicalgraph #lawoflogic #logicalaxiom #logic #truthvalue #liar #ostensiblestatement #axiomoflogic #allliarnoparadox