Terence Tao · @tao
8484 followers · 184 posts · Server mathstodon.xyz@djalbat @holbot All the available talks can be found either on the #IPAM youtube channel https://www.youtube.com/channel/UCGzuiiLdQZu9wxDNJHO_JnA or by navigating to the individual talks in the #MachineAssistedProofs workshop web page https://www.ipam.ucla.edu/programs/workshops/machine-assisted-proofs/?tab=schedule .
Terence Tao · @tao
8484 followers · 184 posts · Server mathstodon.xyz@holbot @djalbat This recent #IPAM #MachineAssistedProofs talk by Jason Rute discusses the state of the art in this direction: https://www.youtube.com/watch?v=P5ew0BrRm_I (also discussed here at https://mathstodon.xyz/@tao/109875787762679762 )
Terence Tao · @tao
8305 followers · 175 posts · Server mathstodon.xyzInspired by the recent #IPAM conference on #MachineAssistedProofs, I wrote a blog post inviting discussion regarding the possibility of automatically generating a logical diagram for a given mathematical paper. https://terrytao.wordpress.com/2023/02/18/would-it-be-possible-to-create-a-tool-to-automatically-diagram-papers/
pablo suárez-serrato · @pablo
7 followers · 15 posts · Server fediunam.siteHoy culmina el programa de #MachineAssistedProofs , al que le podríamos llamar #MatemáticasAutomáticas . En verdad, hay que pensar que «a todo cerdo le llega su San Martín» y que estamos llegando a un cambio de paradigma, al final de un camino. Poco a poco el trabajo, a veces tedioso y a veces complejo, detrás de una demostración matemática se está automatizando. A penas van los conceptos básicos de algunas áreas, pero ahí va la maquinaria creciendo.
#machineassistedproofs #matematicasautomaticas
Applied Geometry Lab · @appliedgeometry
16 followers · 9 posts · Server sigmoid.socialML4PureMath in the #MachineAssistedProofs workshop at #IPAM this week. https://mathstodon.xyz/@tao/109858184238417737
James Smith · @djalbat
8 followers · 32 posts · Server mathstodon.xyzP8's proof can be shortened, in fact. The three statements that appear after the "Hence' can all be omitted. They are there only to make the proof more readable.
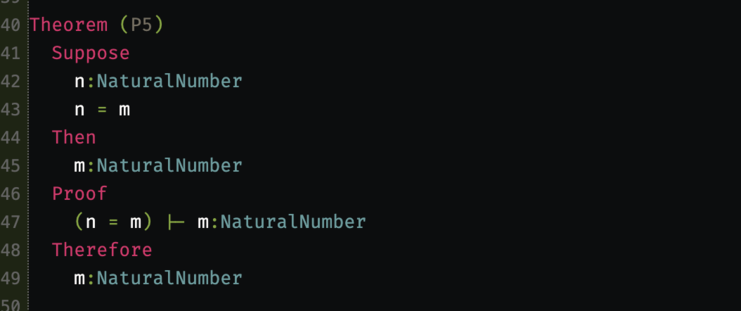
James Smith · @djalbat
8 followers · 31 posts · Server mathstodon.xyzWoop, just this moment finished verifying Peano's axioms bar the last. I think P5 and P7 are my favourites for their simplicity. P8 is probably the most interesting as a proof, however.
On to deriving the Principal of Induction next, which has been a goal for several years now.
James Smith · @djalbat
8 followers · 29 posts · Server mathstodon.xyzExplicit type inference is now working. Automatic or implicit type inference was not going to work for technical reasons.
pablo suárez-serrato · @pablo
7 followers · 12 posts · Server fediunam.siteEsta semana estaré participando en #IPAM en #UCLA en un programa de #MachineAssistedProofs . se tratará la automatización de demostraciones matemáticas. Mi primera experiencia con esto fue cuando en 2015 demostramos, con Luis García-Naranjo y Ramón Vera, que toda 4-variedad lisa admite una estructura de Poisson. Para la prueba tuvimos que apoyarnos en calculos que realizó un programa en Mathematica, de cómputo simbólico. https://link.springer.com/article/10.1007/s11005-015-0792-8
#ipam #ucla #machineassistedproofs
Terence Tao · @tao
8165 followers · 144 posts · Server mathstodon.xyzThe #IPAM workshop on #MachineAssistedProofs (which I am the lead organizer of) starts in less than an hour: http://www.ipam.ucla.edu/programs/workshops/machine-assisted-proofs/ . As an experiment, I plan to make some occasional posts on the workshop as comments to this post. (For people not already registered, the talks will be made available online one to two weeks after the event.)