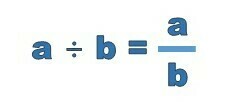#MATH 📈📉 very simply explains America’s 🇺🇸 #Homeless problem 👉 https://vm.tiktok.com/ZT8jRQ6k7/

Cercles inscrits
#geogebra #sketch #random #grid #math

#Calculemus: Demostraciones con Lean4: "Si x,y,z ∈ ℕ, entonces x divide a yxz". https://www.glc.us.es/~jalonso/calculemus/12-sep-23/ #ITP #Lean4 #Math

أعمل حاليا على دعم المعادلات الرياضياتية العربية في ليبرأوفيس، النتائج مبشرة حتى الآن.

#LibreOffice #Arabic #math

Proof that 0=∞:

Given:
1
— = 0
∞

Rotate by π/2:
-18 = 0

Add 8:
-10 = 8

Rotate by π/2:
0
— = ∞
1

Thus, 0=∞. 😎

#math

@nilikm Probably a #Russian troll farm bot 🤖, but no doubt upsetting nonetheless.

The real and bigger problem on both sides of the #US_Canada border is #CowardlyConservatives who are afraid to #resist #fascists.

The #MATH solution is for liberals and independents to join sane conservatives and to #PrimaryFromTheCenter. 🌊 💩 👉 🚽

Today I asked students what properties they thought \( \approx \). They quickly realized that first they needed to think about which properties they should consider for \( \approx \). I was impressed when, listening in on one conversation, I heard a student tell her classmate "I think it's more like = than like +."

#math #MathEd

"Des cercles bien rangés à droite"

#geogebra #sketch #random #grid #math

Avi Wigderson
Abel Prize laureate 2021
Humans and Machines (HLF2022)
#math
https://youtu.be/FHTiMOmB6hM?si=GWOWQsoRKlmsoJmN

I'm thrilled to announce the inaugural release of Functor Network (https://www.functor.network), a blog platform for mathematicians. We have successfully implemented the most fundamental functionality and essential features.

On Functor Network, you can create a post in either markdown or LaTeX format. Regardless of the format you choose, important features for mathematical content like automatic references, bibliography, LaTeX packages, and theorem environments are all fully supported. All you need to focus on is your content.

Different from Mathstodon, Functor Network is more suitable for relatively long and mathematically intensive posts, such as some math notes or research progress reports.

#math #blog #platform

⬆️ #womenInSTEM #math #mathEducation

What are good references for #GroupTheory beyond the introduction? @ProfKinyon?

#Math

☆ Π MTH ~χχ~✧⁰⁰²⁰ Π∞ßτ З¹⁸² ⁰⁰כ

Crystallization Theorem

The expression \( \sqrt{ 𝑎 + 𝑏\sqrt{𝑐} } \) can be simplified to \( \pm \left( \Phi + \Psi\sqrt{c} \right) \) where \( \Phi \) is the solution of the bi-square \( \Phi^4 - a\Phi^2 + \frac{1}{4}b^2c = 0 \) and \( \Psi = \frac{b}{2\Phi} \)

... Example ...
\[ \sqrt{ 6 + 4\sqrt{2} } \]
Consequently
\[
\begin{align}
a &= 6 \\
b &= 4 \\
c &= 2 \\
\end{align}
\]
Resulting in the bi-square equation
\[ \Phi^4 - 6\Phi^2 + 8 = 0 \]
By doing \( t=\Phi^2 \) we have
\[ t² - 6t + 8 = 0 \]
Solving...
\[
\begin{align}
t &= \frac{ -(-6) \pm \sqrt{(-6)^2 - 4×1×8} }{2×1} \\
&= \frac{6 \pm \sqrt{36 - 32}}{2} \\
&= \frac{6 \pm \sqrt{4}}{2} \\
&= \frac{6 \pm 2}{2} \\
\end{align}
\]
\[ \therefore \]
\[
\begin{align}
t_+ &= 4 \\
t_- &= 2 \\
\end{align}
\]
Remembering...
\[ t=\Phi^2 \]
We have
\[
\begin{align}
\Phi_{++} &= +\sqrt{t_+} = +\sqrt{4} = +2 \\
\Phi_{-+} &= -\sqrt{t_+} = -\sqrt{4} = -2 \\
\Phi_{+-} &= +\sqrt{t_-} = +\sqrt{2} = +\sqrt{2} \\
\Phi_{--} &= -\sqrt{t_-} = -\sqrt{2} = -\sqrt{2} \\
\end{align}
\]
Consequently
\[
\begin{align}
\Psi_{++} &= \frac{b}{2\Phi_{++}} = \frac{4}{2×2} = 1 \\
\Psi_{-+} &= \frac{b}{2\Phi_{-+}} = \frac{4}{2×(-2)} = -1 \\
\Psi_{+-} &= \frac{b}{2\Phi_{+-}} = \frac{4}{2×\sqrt{2}} = +\sqrt{2} \\
\Psi_{--} &= \frac{b}{2\Phi_{--}} = \frac{4}{2×(-\sqrt{2})} = -\sqrt{2} \\
\end{align}
\]
\[ \therefore \]
\[
\begin{align}
\sqrt{ 6 + 4\sqrt{2} } &= +\left( 2 + \sqrt{2} \right) \\
&= -\left( 2 + \sqrt{2} \right) \\
\end{align}
\]
\[ Water \space is \space Water \]
\[ □ \]

Videre+

☆ Π MTH ~χ¡χ~✧⁰⁰¹⁹ Π∞ßτ З¹⁸¹ ⁰⁰כ

https://mathstodon.xyz/@JacquesTimmermans/111007237535594404

αΩ

~ ∇ ~

#math #art

[ BRAZIL \( \cdot \) З¹⁸² LND Lunedì χ¡ Settembre MMχχ¡¡¡ ⁰⁰כ ]

☆ Π MTH ~χχ~✧⁰⁰²⁰ Π∞ßτ З¹⁸² ⁰⁰כ

Crystallization Theorem

The expression \( \sqrt{ 𝑎 + 𝑏\sqrt{𝑐} } \) can be simplified to \( \Phi + \Psi\sqrt{c} \) where \( \Phi \) is the solution of the bi- square \( \Phi^4 - a\Phi^2 + \frac{1}{4}b^2c = 0 \) and \( \Psi = \frac{b}{2\Phi} \)

... Example ...
\[ \sqrt{ 6 + 4\sqrt{2} } \]
Consequently
\[
\begin{align}
a &= 6 \\
b &= 4 \\
c &= 2 \\
\end{align}
\]
Resulting in the bi-square equation
\[ \Phi^4 - 6\Phi^2 + 8 = 0 \]
By doing \( t=\Phi^2 \) we have
\[ t² - 6t + 8 = 0 \]
Solving...
\[
\begin{align}
t &= \frac{ -(-6) \pm \sqrt{(-6)^2 - 4×1×8} }{2×1} \\
&= \frac{6 \pm \sqrt{36 - 32}}{2} \\
&= \frac{6 \pm \sqrt{4}}{2} \\
&= \frac{6 \pm 2}{2} \\
\end{align}
\]
\[ \therefore \]
\[
\begin{align}
t_+ &= 4 \\
t_- &= 2 \\
\end{align}
\]
Remembering...
\[ t=\Phi^2 \]
We have
\[
\begin{align}
\Phi_{++} &= +\sqrt{t_+} = +\sqrt{4} = +2 \\
\Phi_{-+} &= -\sqrt{t_+} = -\sqrt{4} = -2 \\
\Phi_{+-} &= +\sqrt{t_-} = +\sqrt{2} = +\sqrt{2} \\
\Phi_{--} &= -\sqrt{t_-} = -\sqrt{2} = -\sqrt{2} \\
\end{align}
\]
Consequently
\[
\begin{align}
\Psi_{++} &= \frac{b}{2\Phi_{++}} = \frac{4}{2×2} = 1 \\
\Psi_{-+} &= \frac{b}{2\Phi_{-+}} = \frac{4}{2×(-2)} = -1 \\
\Psi_{+-} &= \frac{b}{2\Phi_{+-}} = \frac{4}{2×\sqrt{2}} = +\sqrt{2} \\
\Psi_{--} &= \frac{b}{2\Phi_{--}} = \frac{4}{2×(-\sqrt{2})} = -\sqrt{2} \\
\end{align}
\]
\[ \therefore \]
\[
\begin{align}
\sqrt{ 6 + 4\sqrt{2} } &= +\left( 2 + \sqrt{2} \right) \\
&= -\left( 2 + \sqrt{2} \right) \\
\end{align}
\]
\[ Water \space is \space Water \]
\[ □ \]

Videre+

☆ Π MTH ~χ¡χ~✧⁰⁰¹⁹ Π∞ßτ З¹⁸¹ ⁰⁰כ

https://mathstodon.xyz/@JacquesTimmermans/111007237535594404

αΩ

~ ∇ ~

#math #art

[ BRAZIL \( \cdot \) З¹⁸² LND Lunedì χ¡ Settembre MMχχ¡¡¡ ⁰⁰כ ]

The best A – A ≠ 0 paradox
Source : Youtube / Mathologer

https://www.youtube.com/watch?v=VO2A6I3Woos
#mathematics #math #maths

Mathématiques pratiques et éloquence latine : De arte supputandi (1522), premier livre de mathématiques imprimé en Angleterre
Source : CNRS - Image des mathématiques / Kent, Deborah

https://images.math.cnrs.fr/Mathematiques-pratiques-et-eloquence-latine.html
#mathématiques #maths #math

1/4
#MathsMonday
1917 (iii) - Terms included in denominator
My investigation into (alleged) changes in #Mathematics rules in 1917 started with claims that the number of terms included in the denominator of a #Math expression was changed in 1917 (though I've yet to find any actual evidence of this - let me know if you have a reference for it). Some mentioned Lennes' letter, yet his letter says nothing at all about this! For now, let's assume it's true and see what that would mean for #Maths...

FIMO: A challenge formal dataset for automated theorem proving. ~ Chengwu Liu et als. https://arxiv.org/abs/2309.04295 #ITP #LeanProver #Math

Making the impossible possible: Construction of the Tribar with @geogebra; e.g, as an intro to working with GG 3D.

German: https://geogebra.org/m/bmecabaf
English: https://geogebra.org/m/wwn4desn

#math #mathEd #bildung #geometry

#Calculemus: Demostraciones con Lean4: "En ℝ, |a| – |b| ≤ |a – b|". https://www.glc.us.es/~jalonso/calculemus/11-sep-23/ #ITP #Lean4 #Math