A friend of mine watched the movie #Oppenheimer, so I asked if John von Neumann was in it. He wasn't, which is maybe because he was not a permanent part of the Manhattan project, but "only" a consultant who spent most of his time away from Los Alamos.

I found a very good article about his role there:

https://3quarksdaily.com/3quarksdaily/2020/10/what-john-von-neumann-really-did-at-los-alamos.html

That said, #NumericalAnalysis is not mentioned very much.

1/4

We are so happy when our visitors publish their papers connected to their projects at ESI like our current Junior Research Fellow, Sergio Alejandro Gómez Macías.

(the figure below comes from the second article and the authors gave us permission to use that for this tweet)

Sergio Gómez, Andrea Moiola, Ilaria Perugia, Paul Stocker: On polynomial Trefftz spaces for the linear time-dependent Schrödinger equation.

https://arxiv.org/pdf/2306.09571.pdf

Sergio Gómez, Lorenzo Mascotto, Ilaria Perugia: Design and performance of a space-time virtual element method for the heat equation on prismatic meshes.

https://arxiv.org/pdf/2306.09191.pdf

#NumericalAnalysis 🔢

@univienna

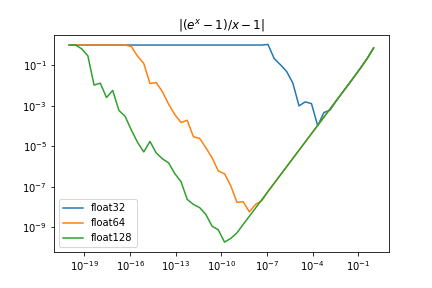
Today I learned that what NumPy calls float128 is not the same as what IEEE calls binary128 and what I call quad precision. Sad.

Instead, NumPy's float128 is what I call extended precision (80 bits).

#FloatingPoint #numpy #NumericalAnalysis

Why Death Valley Is Full Of Polygons [salt flats, deserts, and dry lakes]
--
https://physics.aps.org/articles/v16/31 <-- shared article
--
https://doi.org/10.1103/PhysRevX.13.011025 <-- shared paper
--
#GIS #spatial #mapping #spatialanalysis #model #modeling #salt #polygons #tiling #saltflats #saltdeserts #convection #research #chemistry #water #hydrology #soil #evaporation #evapotranspiration #precipitation #solution #salinity #DeathValley #numericalanalysis #numericalmodeling #numericalsimulation #simulation #groundwater

My thoughts keep turning back to the OWNA (One World Numerical Analysis) talk of Daan Huybrechs a few weeks ago. Most of numerical analysis is built on approximating functions in finite-dimensional spaces:
\[ f(x) \approx \sum_i a_i \varphi_i(i) \],
where 𝑓 is the function we want to approximate and φᵢ are easy functions like polynomials. In the standard setting, the φᵢ form a basis. The talk explained why you sometimes want to add some more "basis" functions, which destroys the linear independence of the φᵢ so that they are no longer a basis. The main topic was the theory behind this.

As motivation, consider the square root function on [0, 1]. This is not analytic at x=0 and approximation by polynomials does not converge fast. However, you can get fast convergence (root exponential IIRC) if you use rational functions. More generally, the solution of Laplace's equation on a domain with re-entrant corners has singularities at the corners. The lightning method uses an overcomplete "basis" of polynomials and rational functions, which converges fast.

It's one of those talks that I wished I understood fully, but it would take me over a month of sustained effort or more to do so. Hopefully I will find an excuse to immerse myself in the topic.

#ApproximationTheory #NumericalAnalysis

In #optimization and solving least-squares, I found that SVD with a smooth cutoff is identical to the damped Levenberg-Marquardt step, see updated note here
https://stephenbrooks.org/ap/report/2015-3/svdboundedsolve.pdf
#maths #computing #numericalanalysis

This particular smoothed solution is also the exact least squares minimum restricted to a sphere of a certain radius.

More info on Levenberg-Marquardt:
https://en.wikipedia.org/wiki/Levenberg%E2%80%93Marquardt_algorithm

After a long introduction in the course of Numerical Analysis, we started to check numerical differentiation and today we'll start with the finite difference method. Today we will work with the Heat Equation in a rod
\[ {\partial u \over \partial t } = \alpha {\partial ^2 u \over \partial x^2},\]
where \[ \alpha \] is the thermal diffusivity constant.
#NumericalAnalysis

Does anybody know if there is an existing tool to verify which of two numerical expressions is more accurate in a given range, possibly including the computational cost?
I usually write my own test code in C or C++, but I would love to know if there is an existing framework for this.

#numericalAnalysis #accuracy #precision #performance #askFedi

Today I found a nice open-access text book for a first course in #NumericalAnalysis, written by Kees Vuik (Delft) et al. It treats interpolation and numerical differentiation, root-finding methods for nonlinear equations, quadrature, integration of ODEs, and finite differences for two-point BVPs and the heat equation. Link: https://textbooks.open.tudelft.nl/textbooks/catalog/book/57

Thanks also to the excellent NA Digest newsletter where this was announced: https://netlib.org/na-digest-html/

*Numerical Methods that Work*, Forman Acton (AMS 1990) https://archive.org/details/numericalmethods00form

#AppliedMathematics #NumericalAnalysis

HT @tpfto

RT @CSiettos
#datadriven #numericalanalysis & #control of #uncertain #complexsystems
Look Ma!: "Equation-free, Variable-free!". Check out how in our new paper in @ElsevierPhysics #JournalComputationalPhysics here:https://www.sciencedirect.com/science/article/pii/S0021999123000487 #machinelearning #manifoldlearning #dynamicalsystems

The answer is a definite “yes.” Hamming named his E as “the shift operator”. If we read Powell’s proof on the convergence (Th. 6.3) and smoothness (Th. 6.4) carefully, and follow the smoothness proof to higher derivatives, we see that the use of binomials (clearly emphasized in Hamming), involves rather tedious shifting of summation indices.

Hamming obviously the engineer, eliding the extra work as part of a subroutine!

#NumericalAnalysis #ApproximationTheory

it seems to me that the operator equation given by Hamming (1989) Ch6 Sec7 is closely related, if not the same as, the Bernstein operator shown in Powell (1981) Eq 6.23

Can someone familiar with #ApproximationTheory or #NumericalAnalysis confirm?

Dover did a nice job reprinting Hamming’s book, but I wish they preserved or appended a citation listing. There’s no bibliography or reference index at all!

it seems to me that the job operator equation given by Hamming (1989) Ch6 Sec7 is closely related, if not the same as, the Bernstein operator shown in Powell (1981) Eq 6.23

Can someone familiar with #ApproximationTheory or #NumericalAnalysis confirm?

Dover did a nice job reprinting Hamming’s book, but I wish they preserved or appended a citation listing. There’s no bibliography or reference index at all!

I really enjoyed the paper

Oteo & Ros, Why Magnus expansion?, URL: https://doi.org/10.1080/00207160.2021.1938011 (paywall)

and not just because it cites a paper of mine (though it does help!)

It's a historical/personal reflection on the Magnus expansion, a series solution to the differential equation \( x'(t) = A(t) x(t) \) which I describe below the fold. (1/n, n≈7)

#MagnusExpansion #DifferentialEquations #MatrixExponential #QuantumMechanics #LieGroups #NumericalAnalysis #GeometricNumericalIntegration

Today I attended an excellent seminar by Yunan Yang (ETH Zürich) titled "Optimal transport for learning chaotic dynamics via invariant measures" in the #NumericalAnalysis and #ScientificComputing series in Manchester.

Many interesting ideas and a lot to unpack, so I can't do it justice, but here is a summary.

#OptimalTransport #DynamicalSystems #ParameterIdentification #InverseProblems

Hello everybody, here is my #introduction.

I am Jitse (he/him), originally from the Netherlands but working in the School of Mathematics at the University of #Leeds, UK for 10+ years. Research interests: #NumericalAnalysis and #DynamicalSystems. Lately working on Fourier extension, geometric numerical integration and applications in particle methods in plasma physics and compartments models in chemistry. I contribute to #Spyder, an open=source IDE for Python geared towards scientists.