heno · @toivcode0227
1 followers · 390 posts · Server mastodon.world3/
The authors provide important definitions and theorems on critical edges, local minima, and selective Rips complexes, and caution that certain assumptions are necessary for their results to hold. #Topology #RipsComplexes #PersistentHomology #ComputerScience #TopologicalDataAnalysis
#topology #ripscomplexes #persistenthomology #computerscience #topologicaldataanalysis
Julien Tierny · @JulienTierny
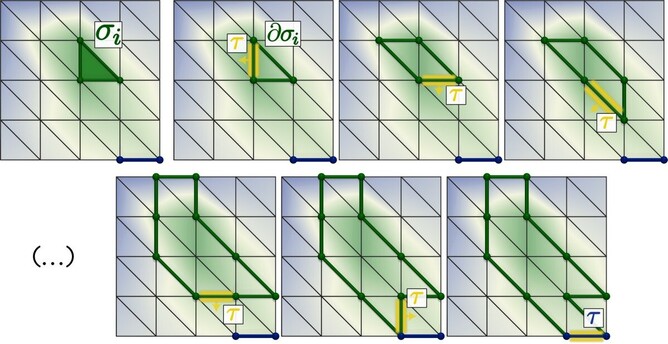
29 followers · 12 posts · Server fosstodon.orgTo compute #PersistentHomology, one needs to check, for each d-simplex σi of a filtration, if it "fills" a (d-1)-dimensional hole, i.e. if its boundary ∂σi is homologous to a non-trivial (d-1)-cycle created on an unpaired (d-1)-simplex (blue).
👇
https://arxiv.org/abs/2206.13932
#TopologicalDataAnalysis #Visualization #DataScience
Funded by the European Research Council (ERC) (project TORI, https://erc-tori.github.io/)
#persistenthomology #TopologicalDataAnalysis #visualization #datascience
Julien Tierny · @JulienTierny
22 followers · 7 posts · Server fosstodon.orgTwo p-cycles a and b are "homologous" (i.e. belong to the same #Homology class) if there exists a (p+1)-chain c, such that b = a + ∂c (mod-2 sum)
👇
https://arxiv.org/abs/2206.13932
#TopologicalDataAnalysis #TopologyToolKit #PersistentHomology #Visualization #DataScience #MachineLearning
#homology #TopologicalDataAnalysis #topologytoolkit #persistenthomology #visualization #datascience #machinelearning
Julien Tierny · @JulienTierny
21 followers · 5 posts · Server fosstodon.orgCheck out our new paper with
@_gosiao
on the #TopologicalDataAnalysis of magnetic currents in molecules with the #TopologyToolKit 👇
Accepted to
@PCCP
https://arxiv.org/abs/2212.08690
#PersistentHomology #visualization #compchem #paraview
#TopologicalDataAnalysis #topologytoolkit #persistenthomology #visualization #compchem #paraview
Julien Tierny · @JulienTierny
18 followers · 3 posts · Server fosstodon.orgTopological persistence is an importance measure in #PersistentHomology, with a strong practical utility for noise removal in various applications: #Imaging, #Clustering, #ClimateScience, #Geophysics, #MaterialScience and more! 👇
https://arxiv.org/pdf/2206.13932
#TopologicalDataAnalysis
#persistenthomology #imaging #clustering #climatescience #geophysics #materialscience #TopologicalDataAnalysis