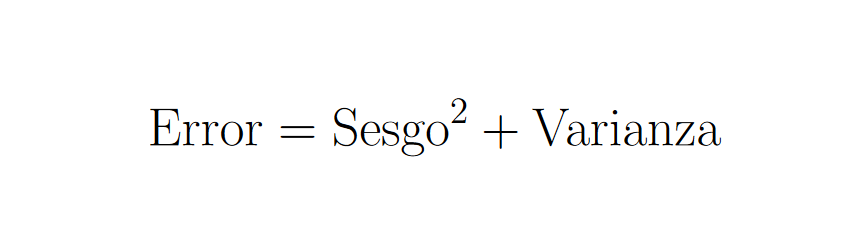Picanúmeros · @Picanumeros
1755 followers · 716 posts · Server mathstodon.xyz¡Espero que os haya molado la explicación y el pequeño quiz que hicimos! Si os ha gustado, los impulsos al primer post del hilo son bienvenidos, y los comentarios son todavía más bienvenidos ☺️ #PicaMuestraGrande
Picanúmeros · @Picanumeros
1755 followers · 716 posts · Server mathstodon.xyzAsí que, en definitiva, si alguna vez dudáis sobre si un tamaño de muestra es grande o pequeño (sin sesgos de por medio), no contéis con la fracción de muestreo: fijaos directamente en el tamaño de la muestra, sin más...
... con algunos matices. Diferentes tipos de muestreo pueden dar lugar a varianzas diferentes que pueden ser mayores o menores que la aquí expuesta.
Y, sobretodo, a partir de ciertos tamaños de muestra, la ganancia (marginal) es muy, muy, muy pequeña. Pero eso ya os lo cuento otro día 🤭
Picanúmeros · @Picanumeros
1755 followers · 716 posts · Server mathstodon.xyz¡Eso es lo que está pasando aquí!
En las opciones a) y b) se sacaba a un 10% de la población, pero como en la opción a) la muestra era más grande, muchos os decantasteis por ella.
Esto tiene parte de cierto, aunque no convierte a la opción a) en la más precisa. Pero vais bien encaminados.
La opción más precisa es la opción c).
En ese caso, se saca sólo a un 0.001% de la población, pero como la muestra es taaan grande en comparación con las otras... esa bajísima fracción de muestreo se termina compensando y produciendo una precisión mucho mayor.
Picanúmeros · @Picanumeros
1755 followers · 716 posts · Server mathstodon.xyzFijaos que en la segunda parte el tamaño de muestra está en el denominador.
Esto hace que, a medida que aumenta la muestra, este término se va haciendo más pequeñito mucho más rápidamente.
Y como va multiplicando, al final se termina "comiendo" a la corrección por finitud.
(si no os lo creéis, os invito a derivar ambos términos con respecto al tamaño de muestra)
Picanúmeros · @Picanumeros
1755 followers · 716 posts · Server mathstodon.xyzComo podéis ver, hay dos partes:
· La denominada corrección por finitud, donde tenemos en cuenta el porcentaje de la población que hemos conseguido seleccionar para la muestra
· La variabilidad de la propia característica a estudiar, dividida entre el tamaño de muestra (!)
Picanúmeros · @Picanumeros
1755 followers · 716 posts · Server mathstodon.xyzComo aquí dijimos que las muestras no proporcionaban sesgo, ese término lo podemos eliminar, por lo que la precisión depende sólo de la varianza.
Y la varianza en la estimación de un porcentaje, en una muestra aleatoria simple, tiene una fórmula concreta.
Es esta:
Picanúmeros · @Picanumeros
1755 followers · 716 posts · Server mathstodon.xyzLa precisión de una estimación depende de dos elementos que se suman entre sí: el #sesgo y la #varianza.
El sesgo se refiere a errores sistemáticos que podamos estar cometiendo.
La varianza se refiere a la incertidumbre de estar usando una muestra en vez de toda la población.
#picamuestragrande #varianza #Sesgo
Picanúmeros · @Picanumeros
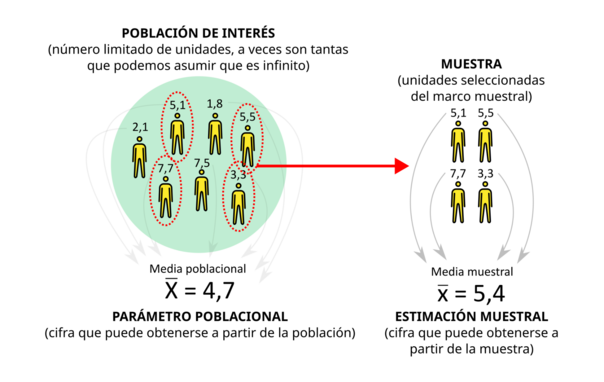
1755 followers · 716 posts · Server mathstodon.xyzNuestro objetivo en las tres situaciones era hacer estimaciones.
Una estimación consiste en acercarnos lo máximo posible a una cantidad real de una población (en este caso, un porcentaje de votantes a un partido) utilizando los datos obtenidos de una muestra de esa población.
Picanúmeros · @Picanumeros
1747 followers · 702 posts · Server mathstodon.xyzDe acuerdo, pues tal y como prometí ayer, se viene hilo explicando y justificando la respuesta correcta a la consulta de antes de ayer (la cual podéis ver en este enlace: https://mathstodon.xyz/@Picanumeros/110793179804408578)
¿Vale más coger una gran fracción de la población cuando hacemos una encuesta, o más bien se trata simplemente de coger una muestra grande?
Usaré el HT #PicaMuestraGrande para el hilo, por si lo queréis silenciar.
Se viene turrita de domingo sobre #estadistica y #muestreo, casi ná! 👇
#muestreo #estadistica #picamuestragrande