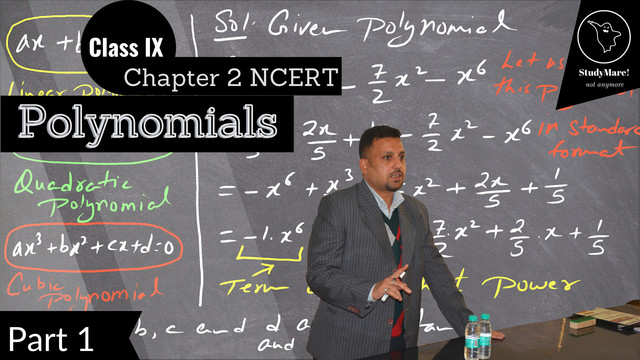@rwxrwxrwx
I wrote this function #'LAMBDAISE that turns a cl-buchberger:polynomial into an unevaluated lambda form at run time. I feel like this is going to have a more elegant expression, but I figure if
the lambdaiseing is happening offline it's okay. What do you think? What do other #CommonLisp #lisp users think? #polynomials
I can use this to modulate period of some beeps, but I'll do that in about 10 hours.

#100daystooffload on codes for turning symbolic polynomials into lambda forms

So....#Lagrange #polynomials. They are pretty dang clever and pretty dang amazing. You can get an analytic (if that's the word I want) polynomial fit! That you can take a continuous derivative!

For arbitrary data, I can see why it might not work.

But for a physical object that actually is moving according to a 2nd-order kinematics (piecewise--really 3rd-order overall) but all you have data for the the first two orders, it might be a good way to recover the higher order(s).

#math #numerical

(I know someone will tell me, so I'll tell myself. If I have position and velocity, I could be solving for the second derivative instead of the first. But maybe I should jump right to lagrange #polynomials in case I have do unequally spaced data later...)

If you need to solve symbolic #math problems in #Python code, check out the complete #solving guide for SymPy #computer #algebra package I wrote ten pages on topics such as systems of #equations, ordinary #differential equations, #polynomials, #inequalities, #matrix equations, and Diophantine equations, and numerical solving. https://docs.sympy.org/dev/guides/solving/index.html

Since I was teaching orthogonal #polynomials (OPs), I asked my class whether they’d read Great Expectations by #Dickens, which you may remember had APs :)

I have a conjecture about how the moments of the roots of a polynomial
(taken as a distribution) are related to the moments of the roots of
its first derivative -- I hope the Mathstodon community can help me
prove or disprove it! @johncarlosbaez I'm looking at you :)
#polynomials #roots #rootrelations (0/7)

#Avocado themed #complex #polynomials

Fun with #complex #polynomials

My new session, Part 1 of Chapter 2 - Polynomials, based on NCERT is live for Class IX Mathematics students, targeted to help Maths students of CBSE, ICSE and other boards. https://youtu.be/jrVXB40HiCc #math #polynomials #mathematics #students #concepts

Challenge: Given a 33 bit shift register based random number generator, shifting 32 times to make a random integer, we observe that a given value will always appear twice in the sequence. Generally unevenly spaced. How to find a value which has the closest repeat?

We could run for 2^33 iterations and keep a record in a many gigabyte array, but I imagine there's a better way.

Boosts OK!

@ColinTheMathmo

#math #maths #polynomials #lfsr #prng #pseudorandom