#DifferentialPropositionalCalculus • 6.2
• https://inquiryintoinquiry.com/2020/03/02/differential-propositional-calculus-6/

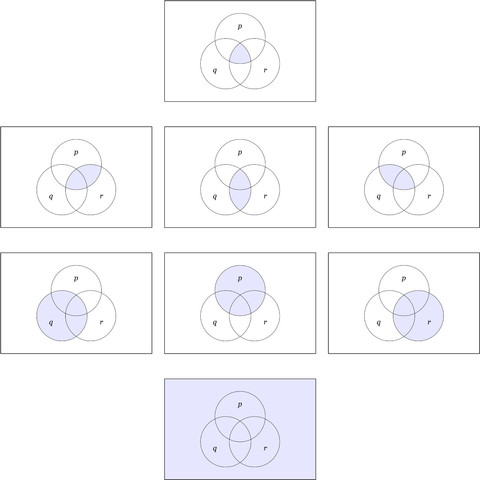
Figure 9. #VennDiagrams for the #PositivePropositions on 3 Variables
• https://inquiryintoinquiry.files.wordpress.com/2020/03/venn-diagrams-e280a2-p-q-r-e280a2-positive-propositions.jpg

Rank 3 (Top). #VennDiagram for the #BooleanProduct or #LogicalConjunction \(pqr.\)

Rank 2. Venn Diagrams for the 3 #BooleanProducts \(pr,\) \(qr,\) \(pq.\)

Rank 1. Venn Diagrams for the 3 #BasicPropositions \(p,\) \(q,\) \(r.\)

Rank 0 (Bottom). Venn Diagram for the #ConstantFunction or the #ConstantProposition \(1.\)

#DifferentialPropositionalCalculus • 6.1
• https://inquiryintoinquiry.com/2020/03/02/differential-propositional-calculus-6/

In a #UniverseOfDiscourse based on 3 #BooleanVariables \(p, q, r\) there are \(2^3 = 8\) #PositivePropositions. Their #VennDiagrams are shown in Figure 9.

\(\text{Figure 9. Positive Propositions} : \mathbb{B}^3 \to \mathbb{B}\)
• https://inquiryintoinquiry.files.wordpress.com/2020/03/venn-diagrams-e280a2-p-q-r-e280a2-positive-propositions.jpg

#DifferentialPropositionalCalculus • 6
• https://inquiryintoinquiry.com/2020/03/02/differential-propositional-calculus-6/

The #PositivePropositions \(\{p:\mathbb{B}^n\to \mathbb{B}\}=(\mathbb{B}^n \xrightarrow{p}\mathbb{B})\) may be written as products:

\[\prod_{i=1}^n e_i~=~e_1 \cdot\ldots\cdot e_n~\text{where}~\left\{\begin{matrix}e_i=a_i\\ \text{or}\\ e_i=1\end{matrix}\right\}~\text{for}~i=1~\text{to}~n.\]

To get a sense of this family's place we'll next draw the #VennDiagrams for the 3 variable case.

#Logic #LogicalGraphs
#DifferentialLogic

#DifferentialPropositionalCalculus • 4.11
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

Linearity, Positivity, Singularity are relative to the basis \(\mathcal{A}.\) #SingularPropositions on one basis do not remain so if new features are added to the basis. A #BasisChange even within the same pairwise options \(\{a_i\}\cup\{\texttt{(}a_i\texttt{)}\}\) changes the sets of #LinearPropositions & #PositivePropositions as both are decided by the choice of #BasicPropositions, in effect choosing a cell as origin.

#Logic

#DifferentialPropositionalCalculus • 4.7
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

The #PositivePropositions \(\{p : \mathbb{B}^n \to \mathbb{B}\} = (\mathbb{B}^n \xrightarrow{p} \mathbb{B})\)may be written as products:

\[\prod_{i=1}^n e_i ~=~ e_1 \cdot \ldots \cdot e_n ~\text{where}~ \left\{ \begin{matrix} e_i = a_i \\ \text{or} \\ e_i = 1 \end{matrix} \right\} ~\text{for}~ i = 1 ~\text{to}~ n.\]

#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions

#DifferentialPropositionalCalculus • 4.5
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

Each of the families — #LinearPropositions, #PositivePropositions, #SingularPrpositions — is naturally parameterized by the coordinate \(n\)-tuples in \(\mathbb{B}^n\) and falls into \(n+1\) ranks, with a #BinomialCoefficient \(\tbinom{n}{k}\) giving the number of propositions having rank or weight \(k\) in their class.

#DifferentialPropositionalCalculus • 4.4
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

Among the \(2^{2^n}\) propositions in \([a_1, \ldots, a_n]\) are several families numbering \(2^n\) propositions each which take on special forms with respect to the basis \(\{a_1, \ldots, a_n \}.\) Three families are especially prominent in the present context, the #LinearPropositions, the #PositivePropositions, and the #SingularPropositions.

#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions