#ITByte: Susceptibility to errors is the single biggest problem holding back #Quantum #Computing from realizing its great promise. Quantum error correction protocols will play a central role in the realisation of quantum computing.

Here is a brief introduction to Quantum Error Correction (#QEC)

https://knowledgezone.co.in/trends/explorer?topic=QEC

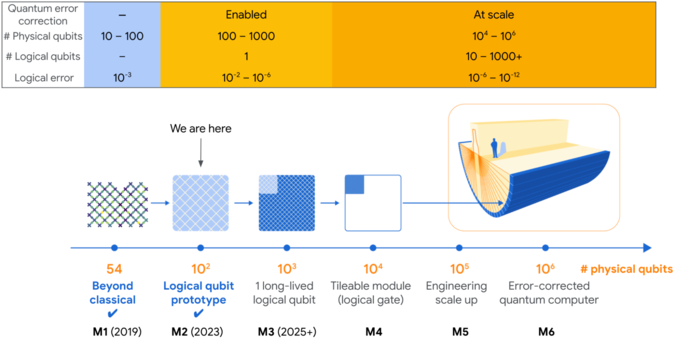
Interesting roadmap from Google to scale error correction, using surface codes, to produce a large-scale fault tolerant quantum computer.
#QuantumComputing #QEC #SurfaceCodes
https://ai.googleblog.com/2023/02/suppressing-quantum-errors-by-scaling.html

A decoding algorithm for non-Abelian anyons

https://arxiv.org/abs/2301.00054

Similar decoding problems have been considered before, but never for arguably the most important case: non-cyclic non-Abelian models with measurement errors.

Here they show evidence for a threshold in this case (specifically for Fibonacci anyons), which lends weight to the idea that they will be fully fault-tolerant.

#quantum #qec

There are a whole bunch of presents under the arXiv tree today.

A GKP repetition code
https://arxiv.org/abs/2212.11397

Recursive MWPM in surface codes
https://arxiv.org/abs/2212.11632

Approximate autonomous QEC
https://arxiv.org/abs/2212.11651

Decoding surface codes with deep reinforcement learning
https://arxiv.org/abs/2212.11890

Repetition cat codes
https://arxiv.org/abs/2212.11927

Also, I missed this from yesterday on fault-tolerant syndrome extraction
https://arxiv.org/abs/2212.10738

#qec #quantum

A method to efficiently simulate Pauli noise on stabilizer states

https://arxiv.org/abs/2212.08677

There's a bit too much maths in their for the week before Christmas, so I'm not going to read this in any depth today. It does look like the method has limitations that would not make it useful for analyzing errors in QEC. Perhaps something for future work.

#qec #quantum

As we've known for many years, surface codes with bit flip noise can be mapped to random bond Ising models.

In this paper the authors expand upon this, to consider also coherent errors and to study entanglement within the system.

The perspective seems mostly to study entanglement phases, rather than QEC itself. But since the Ising mapping has been useful for QEC over the years, we might also find insights here.

https://arxiv.org/abs/2212.08084

#qec #quantum

Randomized benchmarking is a standard tool for benchmarking physical qubits. Assuming that the same will be true for logical qubits is not a big stretch.

But in this paper they show it might not be so easy. The mechanism of QEC can provide effects that violate the assumptions of RB. They admit it's a contrived example, but it's definitely something that needs looking into.

https://arxiv.org/abs/2212.05488

#qec #quan

Using codes based on graph states to deal with photon loss in approaches based on photonic qubits.

https://arxiv.org/abs/2212.04834

#qec #quantum

Between the extremes of error mitigation and full QEC is a mostly undiscovered land. Coherent parity checks are one known landmark, and today's paper is about them
https://arxiv.org/abs/2212.03937

#qec #quantum

Applying some classical coding theory to the problem of adapting to biased noise in quantum codes.

As far as I can tell, they don't actually construct any quantum codes here. But they lay the groundwork for new codes that could be developed in the future

https://arxiv.org/abs/2212.00431

#qec #quantum

An architecture for fault-tolerance with spin qubits!
https://arxiv.org/abs/2212.01550
Definitely deserves more to be said than just that, but today I only have time to do a short one.

#qec #quantum

There's a few papers today!

One on improved methods for fault-tolerant post-selection, to get nice quality magic states without too much overhead
https://arxiv.org/abs/2212.00813

One on variants of the quantum double models (generalizations of the surface code) with strange new properties
https://arxiv.org/abs/2212.01021

And one on using classical LDPC codes for quantum key distribution, tailored to reducing the computational load of the receiver
https://arxiv.org/abs/2212.01121

#qec #quantum

A long awaited paper, exploring how much of what we do in topological codes can be understood as forms of anyon condensation. It specifically focusses on color codes, and find novel ways of doing fault-tolerant gates.

They also discover show that dynamically altering the anyon condensation can lead to Floquet codes.

https://arxiv.org/abs/2212.00042

#qec #quantum
* I have long accepted that 'color codes' are just their name, despite the lack of a 'u'.

When running a quantum algorithm, not all qubits will have gates being applied to them at all times. Algorithms might even have qubits being idle 99% of the time.

In this paper they look at how to fix this. Given surface code blocks arranged in 2D, but with rare non-local connections between blocks, the idling time can be reduced dramatically.

As for exactly how, that will take more careful reading of this detailed paper.

https://arxiv.org/abs/2211.15465
#qec #quantum

QEC should be tailored to abilities and constraints of the hardware it runs on, such as the coupling map and noise.

Motivated by this, the authors of this paper present variants of the surface code, tailored to both the coupling map of IBM Quantum hardware and a bias towards Z type errors

https://arxiv.org/abs/2211.14038

Though IBM hardware doesn't have a bias towards Z errors, this would certainly be useful for, say, spin qubit systems with the same coupling

#quantum #qec

A big paper on twists in fermionic surface codes.

These codes are like the standard qubit surface codes, but built out of Majorana modes rather than qubits.

Twists are essentially lattice defects in a code, which open up new ways to store and manipulate qubits.

Put them together, and it seems you get a broader range of twists than in surface codes, and more efficient storage of logical information.

https://arxiv.org/abs/2211.11777
#qec #quantum

Actually this paper isn't about QEC. But it reminds me of the repetition code in some ways, which is what caught my eye.

https://arxiv.org/abs/2211.11729

There's a thread on it by @MarisOzols here
https://mastodon.online/@MarisOzols@mathstodon.xyz/109386508264751463
(though if you are on the app, you'd probably be better off clicking the handle rather than the link).

#qec #quantum

Quantum error correcting codes often like to give us nice, error-free ways of doing certain gates. But it's never all the gates we need. In this paper, they refer to this as a `conservation of unpleasantness'.

One way around this is to find ways to prepare non-stabilizer states. And in this paper, they propose a new way of doing just that
https://arxiv.org/abs/2211.10046
#qec #quantum

QEC is all about getting encoded qubits that are better than the physical qubits they are made out of, but we are only just about reaching the break-even point.

Today there's a paper on achieving break-even with qubits encoded in photons
https://arxiv.org/abs/2211.09319
Yesterday there was one on achieving break-even with continuous variable states in superconducting circuits
https://arxiv.org/abs/2211.09116
The more standard approaches to QEC have some catching up to do!
#qec #quantum

It's easy to say that you can do QEC with a gigantic lattice of qubits. It's a lot harder to actually build that lattice. And the bigger it is, the more likely there are to be systematic problems that need to be worked around.

Here they look at the details of how to do this, specifically for the surface code. They find that everything works out fine in the end, though there are more details to probe (like doing logical gates).

#qec #quantum
https://arxiv.org/abs/2211.08468