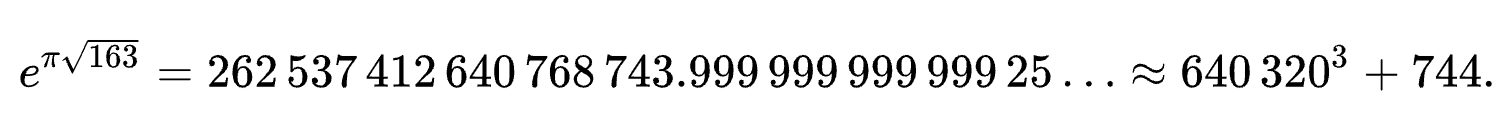The fact there is a :ramanujan: emoji just fills my heart with joy

Thank you #mathstodon for existing

#maths #ramanujan

PPS> #bollywood ending? ... to a #rap: "Twin Primes, Will we know in time?" Maybe some #Ramanujan props amidst the dancing? Some numbered taxis?

#Ramanujan: The Greatest #Mathematical #Prodigy : Medium

Europe spent €600 million to recreate the #Human #Brain in a #Computer. How did it go? : Nature

New #JWST data confirms, worsens the #Hubble #Tension : Big Think

Check our latest #KnowledgeLinks

https://knowledgezone.co.in/resources/bookmarks

I love Ramanujan. He was an amazing person. In 1911 he posed the nested radical problem shown below (or left) in the Journal of the Indian Mathematical Society. When he didn't receive a response he solved it himself.

A few of my notes are here: https://davidmeyer.github.io/qc/nested_radicals.pdf

The LaTeX source is here: https://www.overleaf.com/read/qwhvvhrzrgct

As always, questions/comments/corrections/* greatly appreciated.

#math #maths #nestedradicals #ramanujan

Math geek kid has a #Ramanujan poster; departed dad kept a #Krishna figurine

Not only is the mathematics of Ramanujan's nested radical result cool, but it looks pretty cool as well. LaTeX typesets nested radicals in a nice way too. For an example of both, see Equation (2) in the image.

My notes are here: https://davidmeyer.github.io/qc/nested_radicals.pdf. The LaTeX source is here: https://www.overleaf.com/read/qwhvvhrzrgct.

As always, questions/comments/corrections/* greatly appreciated.

#math #ramanujan

The fascinating Heegner numbers [1] are so named for the amateur mathematician who proved Gauss' conjecture that the numbers {-1, -2, -3, -7, -11, -19, -43, -67,-163} are the only values of -d for which imaginary quadratic fields Q[√-d] are uniquely factorable into factors of the form a + b√-d (for a, b ∈ ℤ) (i.e., the field "splits" [2]). Today it is known that there are only nine Heegner numbers: -1, -2, -3, -7, -11, -19, -43, -67, and -163 [3].

Interestingly, the number 163 turns up in all kinds of surprising places, including the irrational constant e^{π√163} ≈ 262537412640768743.9999999999992500... (≈ 2.6253741264×10^{17}), which is known as the Ramanujan Constant [3].

Some of my notes are here: https://davidmeyer.github.io/qc/galois_theory.pdf. As always, questions/comments/corrections/* greatly appreciated.

#math #galois #gauss #heegnernumber #ramanujan

References
--------------
[1] "Heegner Number", https://mathworld.wolfram.com/HeegnerNumber.html

[2] "Splitting Field", https://mathworld.wolfram.com/SplittingField.html

[3] "Heegner numbers: imaginary quadratic fields with unique factorization (or class number 1).", https://oeis.org/A003173

[4] "Ramanujan Constant", https://mathworld.wolfram.com/RamanujanConstant.html

Every time I see this I have the same reaction: It is amazing how clever Ramanujan was.

My brief notes are here: https://davidmeyer.github.io/qc/nested_radicals.pdf. The LaTeX source is here: https://www.overleaf.com/read/qwhvvhrzrgct.

As always, questions/comments/corrections/* greatly appreciated.

#Ramanujan #nestedradicals #math

#Langlands - The Biggest Project in Modern #Mathematics

https://www.youtube.com/watch?v=_bJeKUosqoY&ab_channel=QuantaMagazine

#LanglandsProgramme #LanglandsProject #NumberTheory #Arithmetic #Math #Maths #Mathematics #Harmonics #HarmonicTheory #Numbers #Ramanujan #Fermat #Wiles #Weil #Frey #Proof #MathematicalProof

Ever notice the number 163 in an unexpected place? Well, Gauss, Ramanujan and many others did. Check out https://en.wikipedia.org/wiki/163_(number) for a brief overview. 163 is a crazy and mysterious thing.

How did I stumble on this? Well, somehow √163 is related to the end of a sequence that Gauss discovered (but couldn't prove) [1] as well as playing a critical role in the "almost integer" that Ramanujan discovered (how? who knows) that is now known as the Ramanujan constant (see the image), and many other things.

Somehow 163 plays a fundamental role in nature.

I wrote a bit about 163 here: https://davidmeyer.github.io/qc/galois_theory.pdf

As always, questions/comments/corrections/* greatly appreciated.

#math #ramanujan

References
--------------
[1] https://en.wikipedia.org/wiki/Heegner_number

Here's another one I've been working on a bit this morning: https://davidmeyer.github.io/qc/nested_radicals.pdf.

As always, questions/comments/corrections/* greatly appreciated.

#math #Ramanujan

How could adding positive integers equal a negative fraction?🤔 🔗 https://www.cantorsparadise.com/the-ramanujan-summation-1-2-3-1-12-a8cc23dea793

Ramanujan's summation: \(1+2+3+\cdots=-\dfrac{1}{12}\)

#RamanujanSummation #Ramanujan #Summation #CantorsParadise #InfiniteSum #NaturalNumbers #NegativeFraction #Fraction #NegativeNumber

How could adding positive integers equal a negative fraction?🤔🔗https://www.cantorsparadise.com/the-ramanujan-summation-1-2-3-1-12-a8cc23dea793\

Ramanujan's summation:
\[1+2+3+\cdots=-\dfrac{1}{12}\]

#RamanujanSummation #Ramanujan #Summation #CantorsParadise #InfiniteSum #NaturalNumbers #NegativeFraction #Fraction #NegativeNumber

Goal: find 𝑓 and 𝑔 such that for all 𝑛∈ℕ, 𝑓(𝑛)=𝑔(𝑛,𝑓(𝑛+1)) and then use this to form an infinite nested expression with a simple value.#Ramanujan #math

Observation:
 𝑛²−1=(𝑛−1)(𝑛+1)
 (𝑛+2)²−1=(𝑛+1)(𝑛+3)

Let \[ \displaylines{f(n)= n(n+2) \\ g(n, m)= n\sqrt{1 + m}} \]

Then:
 𝑓(𝑛+1)=(𝑛+1)(𝑛+3)
And:
 𝑓(𝑛)=𝑔(𝑛,𝑓(𝑛+1))
 𝑓(1)=3
\[ \displaylines{f(1) = 1 \times \sqrt{1 + f(2)} \\ = \sqrt{1 + 2 \sqrt{1 + f(3)}} = \dots}\]
Which gives mysterious identities when you knock the scaffolding out
.
1/2

Today's #MathTopicOfTheDay is the Ramanujan conjecture! It is named after Srinivasa Ramanujan, who was born on this day in 1887. It concerns the Ramanujan tau function, which are the Fourier coefficients of the discriminant modular form (a cusp form of level 1 and weight 12).

https://en.wikipedia.org/wiki/Ramanujan%E2%80%93Petersson_conjecture

1/n

#Math #Mathematics #Ramanujan

On the birth anniversary of #SrinivasaRamanujan, NIILM University honors National Mathematics Day in a tribute to his contributions to mathematics.

#nationalmathematic #NationalMathematicsDay #national #mathematicday #nationalmathematicsday2021 #SrinivasaRamanujan #ramanujan #22december #Ramanujan #nilmuniversity #mathgenius #geniusofmath

On December 1, 1947, English mathematician G. H. Hardy passed away. Hardy is known for his achievements in number theory and mathematical analysis, but also for his 1940 essay on the aesthetics of mathematics, A Mathematician’s Apology, and for mentoring the brilliant Indian mathematician Srinivasa Ramanujan.

http://scihi.org/g-h-hardy/

#maths #historyofscience #cambridge #Ramanujan

Coded a little bit of Basic yesterday, and then a bit of C, and goodness me the C took a lot longer to get right...

Here's a short version:
B=10:N=1:P=1:REPEAT:N=N+1:C=N*N*N:S=B:B=S-1/(C*P):P=C:UNTIL B=S:PRINT SQR(S)

Here's one for simpler Basic dialects:
B=10:P=1:FORN=2TO22:C=N*N*N:S=B:B=S-1/(C*P):P=C:NEXT:PRINT SQR(B)

Here's a version to run in your browser:
https://bbcmic.ro/#%7B%22v%22%3A1%2C%22program%22%3A%22TIME%3D0%5CnREM%20Computer%20Pi%5CnREM%20by%20Ramanujan%2C%20and%20HPMuseum%20thread%2018584%5CnB%3D10%5CnN%3D1%5CnP%3D1%5CnREPEAT%5CnN%3DN%2B1%5CnC%3DN*N*N%5CnS%3DB%5CnB%3DS-1%2F%28C*P%29%5CnP%3DC%5CnPRINT%20%3BN%3B%5C%22%20%5C%22%3BSQR%28S%29%3B%5C%22%20%5C%22%3BABS%28PI-SQR%28S%29%29%5CnUNTIL%20B%3DS%5CnPRINT%20%5C%22done%20in%20%5C%22%3BN%3B%5C%22%3A%20%5C%22%3BSQR%28S%29%5CnPRINT%20TIME%2F100%3B%5C%22%20seconds%5C%22%22%7D

#retrocomputing #BBCmicro #bbcbasic #ramanujan

@ileturia filma ederra eta gogorra.

#Ramanujan​i buruzko liburu hau irakurtzen ari naiz PDF formatuan (hemen HTML formatuan) pertsona berezi eta errepikaezin honen matematikak eta bizitza sakontasun gehiagorekin ezagutzeko: http://www.librosmaravillosos.com/SvirinasaRamanujan/index.html #matematika

« Ramanujan’s Early Work on Continued Fractions »

#history #math #Ramanujan

https://medium.com/cantors-paradise/ramanujans-early-work-on-continued-fractions-b3c6b13eaf5c