#DifferentialPropositionalCalculus • 7.3
• https://inquiryintoinquiry.com/2020/03/05/differential-propositional-calculus-7/

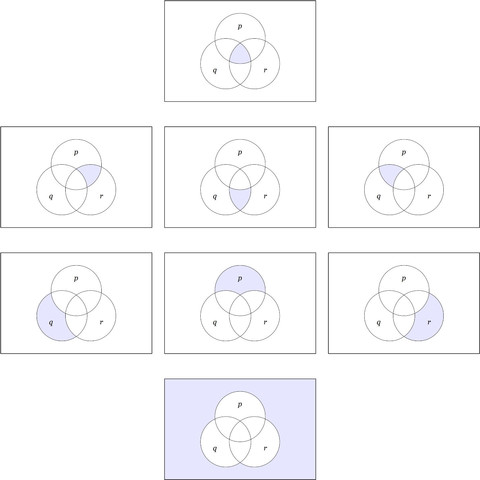
Figure 10. #VennDiagrams for #SingularPropositions on 3 Variables
• https://inquiryintoinquiry.files.wordpress.com/2020/03/venn-diagrams-e280a2-p-q-r-e280a2-singular-propositions.jpg

Rank 3. The cell \(pqr.\)

Rank 2. The 3 cells \(pr\texttt{(}q\texttt{)}, qr\texttt{(}p\texttt{)}, pq\texttt{(}r\texttt{)}.\)

Rank 1. The 3 cells \(q\texttt{(}p\texttt{)(}r\texttt{)}, p\texttt{(}q\texttt{)(}r\texttt{)}, r\texttt{(}p\texttt{)(}q\texttt{)}.\)

Rank 0. The cell \(\texttt{(}p\texttt{)(}q\texttt{)(}r\texttt{)}.\)

#Logic

#DifferentialPropositionalCalculus • 7.2
• https://inquiryintoinquiry.com/2020/03/05/differential-propositional-calculus-7/

In a UniverseOfDiscourse based on 3 #BooleanVariables \(p, q, r\) there are \(2^3 = 8\) #SingularPropositions. Their #VennDiagrams are shown in Figure 10.

\(\text{Figure 10. Singular Propositions} : \mathbb{B}^3 \to \mathbb{B}\)
• https://inquiryintoinquiry.files.wordpress.com/2020/03/venn-diagrams-e280a2-p-q-r-e280a2-singular-propositions.jpg

Related Subjects —
#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions

#DifferentialPropositionalCalculus • 7.1
• https://inquiryintoinquiry.com/2020/03/05/differential-propositional-calculus-7/

The #SingularPropositions \(\{\mathbf{x}:\mathbb{B}^n\to\mathbb{B}\}=(\mathbb{B}^n\xrightarrow{s}\mathbb{B})\) may be written as products:

\[\prod_{i=1}^n e_i~=~e_1\cdot\ldots\cdot e_n~\text{where}~\left\{\begin{matrix}e_i=a_i\\\text{or}\\e_i=\texttt{(}a_i\texttt{)}\end{matrix}\right\}~\text{for}~i=1~\text{to}~n.\]

Related Topics —
#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions

#DifferentialPropositionalCalculus • 7
• https://inquiryintoinquiry.com/2020/03/05/differential-propositional-calculus-7/

In our #Model of #Propositions as #Mappings of a #UniverseOfDiscourse to a set of two values, in other words, #IndicatorFunctions of the form \(f:X\to\mathbb{B},\) #SingularPropositions are those singling out the minimal distinct regions of the universe, represented by single cells of the corresponding #VennDiagram.

Related Subjects —
#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions

#DifferentialPropositionalCalculus • 4.11
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

Linearity, Positivity, Singularity are relative to the basis \(\mathcal{A}.\) #SingularPropositions on one basis do not remain so if new features are added to the basis. A #BasisChange even within the same pairwise options \(\{a_i\}\cup\{\texttt{(}a_i\texttt{)}\}\) changes the sets of #LinearPropositions & #PositivePropositions as both are decided by the choice of #BasicPropositions, in effect choosing a cell as origin.

#Logic

#DifferentialPropositionalCalculus • 4.10
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

The #BasicPropositions \(a_i : \mathbb{B}^n \to \mathbb{B}\) are both linear and positive. So these two kinds of propositions, the linear and the positive, may be viewed as two different ways of generalizing the class of basic propositions.

Related Subjects —
#CoordinatePropositions #SimplePropositions
# LinearPropositions #SingularPropositions

#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions

#DifferentialPropositionalCalculus • 4.8

The #SingularPropositions \(\{\mathbf{x} : \mathbb{B}^n \to \mathbb{B}\} = (\mathbb{B}^n \xrightarrow{s} \mathbb{B})\) may be written as products:

\[\prod_{i=1}^n e_i ~=~ e_1 \cdot \ldots \cdot e_n ~\text{where}~ \left\{ \begin{matrix} e_i = a_i \\ \text{or} \\ e_i = \texttt{(} a_i \texttt{)} \end{matrix} \right\} ~\text{for}~ i = 1 ~\text{to}~ n.\]

Related Subjects —
#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions

#DifferentialPropositionalCalculus • 4.4
• https://inquiryintoinquiry.com/2020/02/25/differential-propositional-calculus-4/

Among the \(2^{2^n}\) propositions in \([a_1, \ldots, a_n]\) are several families numbering \(2^n\) propositions each which take on special forms with respect to the basis \(\{a_1, \ldots, a_n \}.\) Three families are especially prominent in the present context, the #LinearPropositions, the #PositivePropositions, and the #SingularPropositions.

#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions