Famous mathematical theorems illustrated with Midjourney.
Source : Twitter / Tivadar Danka

https://twitter.com/TivadarDanka/status/1649721970886594561
#mathematics #math #maths #theorems #Midjourney

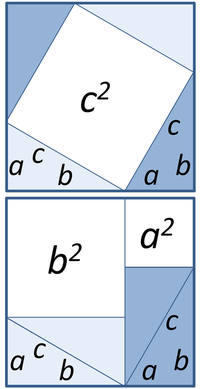
#KnowledgeByte: #Theorems, #Lemmas, #Conjectures and more - Some common definition and brief concepts. #Math101

https://knowledgezone.co.in/posts/601575e622ad6a84e5c3406b

After my previous reply to @erou I remember a couple of *my early theorems*, at the time (10-12 years old) I knew the results were right, but the actual proof come much later when I was in the mid of my B.Sc.

1. \(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots = \sum_{n=1}^\infty 2^{-n} = 1\).

2. \(\frac{1}{2} - \frac{1}{4} + \frac{1}{8} - \frac{1}{16} + \cdots = \sum_{n=1}^\infty (-1)^{n-1} 2^{-n} = \frac{1}{3}\).

#mathematics #theorems #young #science

@erou Wow! I solve that problem (intuitively) when I was like 10 years old (I had a notebook with my theorems... there were about three! five tops, but I was really proud).

Back then I noted that any \(n\)-polygon can be split into \(n-2\) triangles (much later, I found that it is the base of triangulation XD), from there the result is trivial.

#mathematics #theorems #young #science

#mathematics #equations #theorems #fractals #chaos_theory #google #youtube #sumpter #uppsala #sweden #global

Equations built giants like Google. Who’ll find the next billion-dollar bit of maths?

https://www.theguardian.com/commentisfree/2022/jan/24/equations-google-billion-dollar-bits-of-maths#comments