If you've never seen Maxwell's equations before (or just want to review) this is a nice introduction (w/o too much math and including some interesting history): https://www.youtube.com/watch?v=aFYKKSoXC5Y

#math #maths #maxwellsequations #vectorcalculus

#Mechanical #Circuits

As an #EE, I take pride in the fact that, although #ME came before us and #CE before them, much of the #engineering formalism arose in the 19th Century in the electrical context. Much of engineering theories are shared between EE, ME, and CE, and at the core is #VectorCalculus and #AbstractAlgebra. This video shows one such connection.

https://youtu.be/Zv9Q7ih48Uc

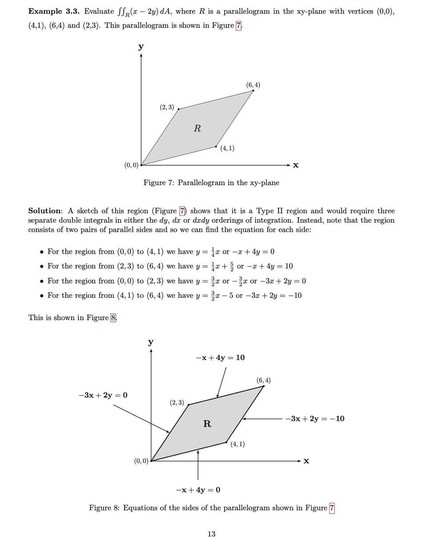
More hacking on my vector calculus notes. This time with a worked double (surface) integral example. The double integral is over a region R but I didn't know how to represent that in FB:

∫∫(x - 2y) dA

This example (ok, I made it up) took more than one page to work through this so I don't know how this will translate to FB...

My notes are here: https://davidmeyer.github.io/qc/vector_calculus.pdf.

As always, questions/comments/corrections/* greatly appreciated.

#math #vectorcalculus

I've been putting in a little more time in on my vector calculus notes: https://davidmeyer.github.io/qc/vector_calculus.pdf. The LaTeX source is here: https://www.overleaf.com/read/fgtfvmgdkbhh.

As always, questions/comments/corrections/* greatly appreciated.

#math #vectorcalculus

GENERALIZED STOKES THEOREM:
The integral of a differential form \(\omega\) over the boundary \(\partial\Omega\) of some orientable manifold \(\Omega\) is equal to the integral of its exterior derivative \(d\omega\) over the whole of \(\Omega\).
\[\displaystyle\int_{\partial\Omega}\omega=\int_\Omega d\omega\]
#VectorCalculus #DifferentialGeometry #MultivariateCalculus #Calculus #StokesTheorem #GeneralizedStokesTheorem #Calculus #FundamentalTheorem #Manifold #Boundary #ExteriorDerivative #Stokes

GENERALIZED STOKES THEOREM:

The integral of a differential form \(\omega\) over the boundary \(\partial\Omega\) of some orientable manifold \(\Omega\) is equal to the integral of its exterior derivative \(d\omega\) over the whole of \(\Omega\).
\[\displaystyle\int_{\partial\Omega}\omega=\int_\Omega d\omega\]
#VectorCalculus #DifferentialGeometry #MultivariateCalculus #Calculus #StokesTheorem #GeneralizedStokesTheorem #Calculus #FundamentalTheorem #Manifold #Boundary #ExteriorDerivative #Stokes

GENERALIZED STOKES THEOREM:
The integral of a differential form \(\omega\) over the boundary \(\partial\Omega\) of some orientable manifold \(\Omega\) is equal to the integral of its exterior derivative \(d\omega\) over the whole of \(\Omega\).
\[\displaystyle\int_{\partial\Omega}\omega=\int_\Omega d\omega\]
#VectorCalculus #DifferentialGeometry #MultivariateCalculus #Calculus #StokesTheorem #GeneralizedStokesTheorem #Calculus #FundamentalTheorem #Manifold #Boundary #ExteriorDerivative #Stokes