Fabrizio Musacchio · @pixeltracker
344 followers · 230 posts · Server sigmoid.socialEliminating the middleman: You can apply the computation of the #Wasserstein distance even more directly in #WassersteinGANs (#WGANs), eliminating the need for a discriminator.
🌎 https://www.fabriziomusacchio.com/blog/2023-07-30-wgan_with_direct_wasserstein_distance/
#wasserstein #wassersteingans #wgans #machinelearning
Fabrizio Musacchio · @pixeltracker
344 followers · 230 posts · Server sigmoid.socialThe #Wasserstein #metric (#EMD) can be used, to train #GenerativeAdversarialNetworks (#GANs) more effectively. This tutorial compares a default GAN with a #WassersteinGAN (#WGAN) trained on the #MNIST dataset.
#wasserstein #metric #emd #generativeadversarialnetworks #GANs #wassersteingan #wgan #mnist #machinelearning
Fabrizio Musacchio · @pixeltracker
338 followers · 223 posts · Server sigmoid.socialApart from #Wasserstein Distance (#EMD), other #metrics also play an important role in #MachineLearning tasks such as #clustering, #classification, and #InformationRetrieval. In this tutorial, you can find a discussion of five commonly used metrics: EMD, #KullbackLeiblerDivergence (KL Divergence), #JensenShannonDivergence (JS Divergence), #TotalVariationDistance (TV Distance), and #BhattacharyyaDistance.
🌎 https://www.fabriziomusacchio.com/blog/2023-07-28-probability_density_metrics/
#wasserstein #emd #metrics #machinelearning #clustering #classification #informationretrieval #kullbackleiblerdivergence #jensenshannondivergence #totalvariationdistance #bhattacharyyadistance
Fabrizio Musacchio · @pixeltracker
338 followers · 223 posts · Server sigmoid.socialThe #Wasserstein distance (#EMD), sliced Wasserstein distance (#SWD), and the #L2norm are common #metrics used to quantify the ‘distance’ between two distributions. This tutorial compares these three metrics and discusses their advantages and disadvantages.
🌎 https://www.fabriziomusacchio.com/blog/2023-07-26-wasserstein_vs_l2_norm/
#wasserstein #emd #swd #l2norm #metrics #OptimalTransport #machinelearning
Fabrizio Musacchio · @pixeltracker
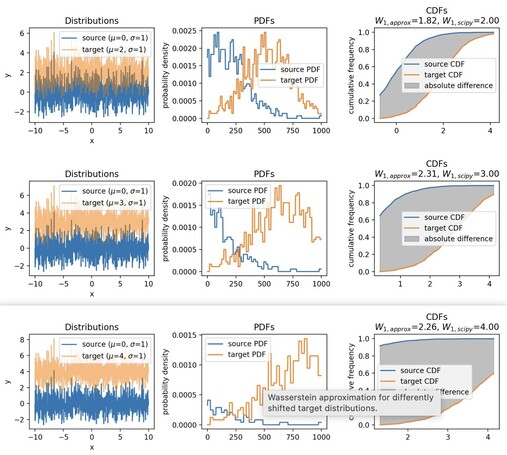
338 followers · 223 posts · Server sigmoid.socialThis tutorial takes a different approach to explain the #Wasserstein distance (#EMD) by approximating the #EMD with cumulative distribution functions (#CDF), providing a more intuitive understanding of the metric.
🌎 https://www.fabriziomusacchio.com/blog/2023-07-24-wasserstein_distance_cdf_approximation/
#wasserstein #emd #cdf #OptimalTransport
Fabrizio Musacchio · @pixeltracker
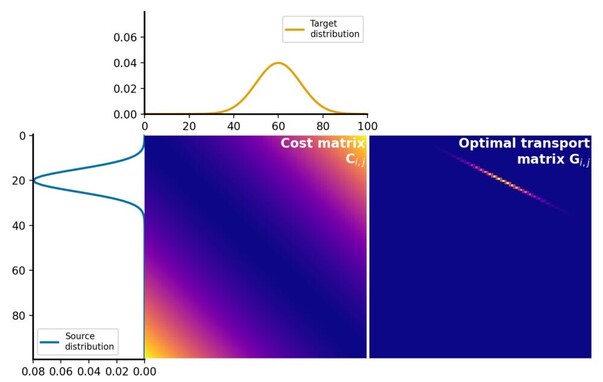
331 followers · 219 posts · Server sigmoid.socialCalculating the #Wasserstein distance (#EMD) 📈 can be computational costly when using #LinearProgramming. The #Sinkhorn algorithm provides a computationally efficient method for approximating the EMD, making it a practical choice for many applications, especially for large datasets 💫. Here is another tutorial, showing how to solve #OptimalTransport problem using the Sinkhorn algorithm in #Python 🐍
🌎 https://www.fabriziomusacchio.com/blog/2023-07-23-wasserstein_distance_sinkhorn/
#wasserstein #emd #linearprogramming #sinkhorn #OptimalTransport #Python
Fabrizio Musacchio · @pixeltracker
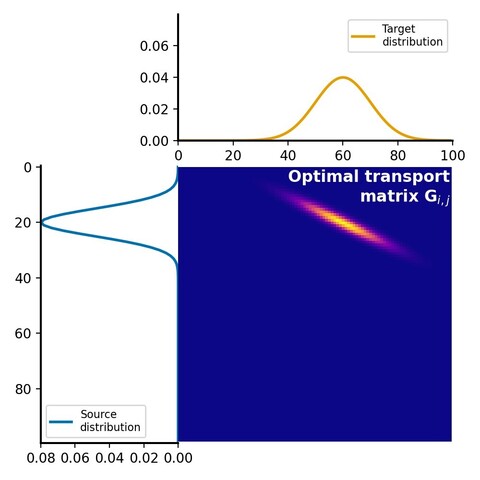
321 followers · 215 posts · Server sigmoid.socialThe #Wasserstein distance 📐, aka Earth Mover’s Distance (#EMD), provides a robust and insightful approach for comparing #ProbabilityDistributions 📊. I’ve composed a #Python tutorial 🐍 that explains the #OptimalTransport problem required to calculate EMD. It also shows how to solve the OT problem and calculate the EMD using the Python Optimal Transport (POT) library. Feel free to use and share it 🤗
🌎 https://www.fabriziomusacchio.com/blog/2023-07-23-wasserstein_distance/
#wasserstein #emd #probabilitydistributions #Python #OptimalTransport
New Submissions to TMLR · @tmlrsub
198 followers · 695 posts · Server sigmoid.socialConvergence of SGD for Training Neural Networks with Sliced Wasserstein Losses
Published papers at TMLR · @tmlrpub
522 followers · 466 posts · Server sigmoid.socialAn Explicit Expansion of the Kullback-Leibler Divergence along its Fisher-Rao Gradient Flow
Carles Domingo-Enrich, Aram-Alexandre Pooladian
Action editor: Murat Erdogdu.
JMLR · @jmlr
672 followers · 268 posts · Server sigmoid.social'Controlling Wasserstein Distances by Kernel Norms with Application to Compressive Statistical Learning', by Titouan Vayer, Rémi Gribonval.
http://jmlr.org/papers/v24/21-1516.html
#compressive #wasserstein #norms
#compressive #wasserstein #norms
Published papers at TMLR · @tmlrpub
507 followers · 293 posts · Server sigmoid.social#fairness #parity #wasserstein
New Submissions to TMLR · @tmlrsub
161 followers · 406 posts · Server sigmoid.socialAn Explicit Expansion of the Kullback-Leibler Divergence along its Fisher-Rao Gradient Flow
Published papers at TMLR · @tmlrpub
506 followers · 282 posts · Server sigmoid.socialSolving a Special Type of Optimal Transport Problem by a Modified Hungarian Algorithm
Yiling Xie, Yiling Luo, Xiaoming Huo
#complexity #wasserstein #transport
Published papers at TMLR · @tmlrpub
495 followers · 211 posts · Server sigmoid.socialOptimizing Functionals on the Space of Probabilities with Input Convex Neural Networks
David Alvarez-Melis, Yair Schiff, Youssef Mroueh
#optimization #gradient #wasserstein
Julien Tierny · @JulienTierny
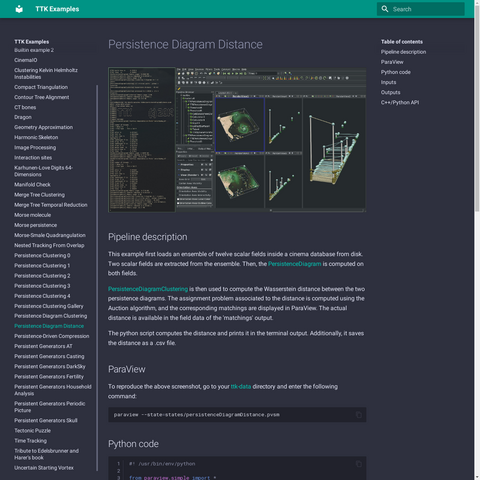
20 followers · 4 posts · Server fosstodon.orgCheckout the new #TopologyToolKit Example Website!
Dozens of #TopologicalDataAnalysis pipelines.
🧑🎓Today, learn how to compute the #Wasserstein distance between the #PersistenceDiagrams of two datasets in 48 lines of #Python👇
https://topology-tool-kit.github.io/examples/persistenceDiagramDistance/
#DataScience #Machinelearning
#topologytoolkit #TopologicalDataAnalysis #wasserstein #persistencediagrams #python #datascience #machinelearning
RTG 2088 · @RTG_2088
13 followers · 13 posts · Server mathstodon.xyzHeinemann, F., Klatt, M. & Munk, A. Kantorovich–Rubinstein Distance and Barycenter for Finitely Supported Measures: Foundations and Algorithms. Appl Math Optim 87, 4 (2023).
https://doi.org/10.1007/s00245-022-09911-x
#article #appliedmathematics #optimization #barycenter #wasserstein #kantorovich-rubinstein
#kantorovich #wasserstein #barycenter #optimization #appliedmathematics #article